Простой трубопровод
Основным элементом любой трубопроводной системы, какой бы сложной она ни была, является простой трубопровод. Классическим определением его будет- простым
трубопроводом является трубопровод, собранный из труб одинакового диаметра и качества его внутренних стенок, в котором движется транзитный поток жидкости, и на котором нет местных гидравлических сопротивлений.
При напорном движении жидкости простой трубопровод работает полным
сечением 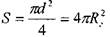 = const. Размер
= const. Размер
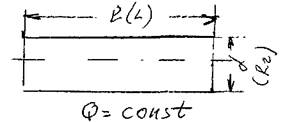 сечения трубопровода (диаметр или величина гидравлического радиуса), а также его протяжённость (длина) трубопровода (/, L) являются основными геометрическими характеристиками трубопровода. Основными технологическими характеристиками трубопровода являются расход жидкости в трубопроводе Q и напор
сечения трубопровода (диаметр или величина гидравлического радиуса), а также его протяжённость (длина) трубопровода (/, L) являются основными геометрическими характеристиками трубопровода. Основными технологическими характеристиками трубопровода являются расход жидкости в трубопроводе Q и напор 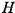 (на головных сооружениях трубопровода, т.е. в его начале). Большинство других характеристик простого трубопровода являются, не смотря на их важность, производными характеристиками. Поскольку в простом трубопроводе расход жидкости транзитный (одинаковый в начале и конце трубопровода), то средняя скорость движения жидкости в трубопроводе постоянна
(на головных сооружениях трубопровода, т.е. в его начале). Большинство других характеристик простого трубопровода являются, не смотря на их важность, производными характеристиками. Поскольку в простом трубопроводе расход жидкости транзитный (одинаковый в начале и конце трубопровода), то средняя скорость движения жидкости в трубопроводе постоянна  . Для установившегося движения жидкости по трубопроводу средняя скорость движения жидкости определяется по формуле Шези:
. Для установившегося движения жидкости по трубопроводу средняя скорость движения жидкости определяется по формуле Шези:
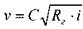 5
5
где:  - скоростной коэффициент Шези,
- скоростной коэффициент Шези,
 - гидравлический радиус сечения, для круглого сечения при полном заполнении жидкостью
- гидравлический радиус сечения, для круглого сечения при полном заполнении жидкостью 
 - гидравлический уклон.
- гидравлический уклон.
Полагая, что весь имеющийся напор на головных сооружениях (в начале) трубопровода тратится на преодоление сил трения в трубопроводе (в простом трубопроводе это потери напора по длине  ), уравнение движения жидкости (Бернулли) примет вид:
), уравнение движения жидкости (Бернулли) примет вид:

Расход жидкости в трубопроводе:
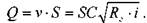
Обозначив: 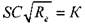 , получим основное уравнение простого трубопровода:
, получим основное уравнение простого трубопровода:
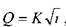
где: К - модуль расхода - расход жидкости в русле заданного сечения при гидравлическом уклоне равном единице (иначе модуль расхода называют расходной характеристикой трубопровода). Другой и более известный вид основного уравнения простого трубопровода получим, решив уравнение относительно напора:

Величину  называют удельным сопротивлением трубопровода,
называют удельным сопротивлением трубопровода, 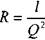 - - его полным сопротивлением
- - его полным сопротивлением
График уравнения простого трубопровода 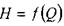 носит название его гидравлической харак
носит название его гидравлической харак 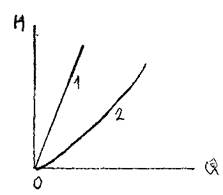 теристики. Вид гидравлической характеристики зависит от режима движения жидкости в трубопроводе: при ламинарном движении жидкости гидравлическая характеристика трубопровода - прямая линия, проходящая через начало координат (1). При турбулентном режиме гидравлическая характеристика - парабола (2).
теристики. Вид гидравлической характеристики зависит от режима движения жидкости в трубопроводе: при ламинарном движении жидкости гидравлическая характеристика трубопровода - прямая линия, проходящая через начало координат (1). При турбулентном режиме гидравлическая характеристика - парабола (2).
Если на трубопроводе собранном из труб одинакового диаметра имеются местные сопротивления, то такой трубопровод можно привести к простому трубопроводу эквивалентной длины 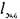

8.3. Сложные трубопроводы
К сложным трубопроводам следует относить те трубопроводы, которые не подходят к категории простых трубопроводов, т.е к сложным трубопроводам следует отнести:
трубопроводы, собранные из труб разного диаметра (последовательное соединение трубопроводов),
трубопроводы, имеющие разветвления: параллельное соединение трубопроводов, сети трубопроводов, трубопроводы с непрерывной раздачей жидкости.
Последовательное соединение трубопроводов. При последовательном соединении
трубопроводов конец предыдущего простого трубопровода одновременно является началом следующего простого трубопровода. В сложном трубопроводе, состоящем из последовательно соединённых простых  трубопроводов, последние в литературе называются участками этого трубопровода. Расход жидкости во всех участках сложного трубопровода остаётся одинаковым Q = const. Общие потери напора во всём трубопроводе будут равны сумме потерь напора во всех отдельных его участках.
трубопроводов, последние в литературе называются участками этого трубопровода. Расход жидкости во всех участках сложного трубопровода остаётся одинаковым Q = const. Общие потери напора во всём трубопроводе будут равны сумме потерь напора во всех отдельных его участках.

 где
где  - потери напора на
- потери напора на  - том участке трубопро-
- том участке трубопро-
вода.
Таким образом, потери напора в трубопроводе, состоящем из последовательно соединённых друг с другом участков равны квадрату расхода жидкости в трубопроводе умноженному на сумму удельных сопротивлений всех участков.
Гидравлическая характеристика трубопровода состоящего из последовательно соединённых участков представляет собой графическую сумму (по оси напоров) гидравлических характеристик всех отдельных участков. На рисунке кривая 1 представляет гидравлическую характеристику 1-го участка трубопровода, кривая 2 - гидравлическую характеристику 2-го участка, кривая 3 - сумму гидравлических характеристик обеих участков.
Сложный трубопровод, состоящий из последовательно соединённых простых трубопроводов можно свести к простому трубопроводу с одинаковым (эквивалентным) диаметром, при этом длины участков будут пересчитываться, чтобы сохранить реальные гидравлические сопротивления участков трубопровода.
Так приведённая длина  - того участка
- того участка  будет:
будет:
'Л 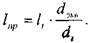
Следует отметить, что величина скоростного напора также зависит от диаметра трубопровода, и при определении приведённой длины участка мы вносим некоторую
ошибку, которая будет тем большей, чем больше разница в величинах фактического и эквивалентного диаметров. В таких случаях можно рекомендовать другой, более сложный способ.
Параллельное соединение трубопроводов. Схема прокладки параллельных трубопроводов используется в тех случаях, когда на трассе магистрального трубопровода есть
участки, где требуется уменьшить гидравлические сопротивления трубопровода (высокие перевальные точки трубопровода) или при заложении трубопровода в трудно 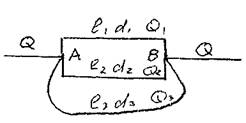 доступных местах (переход через реки и др.). При параллельном соединении трубопроводов имеются две особые точки, называемые точками разветвления. В этих точках находятся концы параллельных ветвей трубопровода (точки А и В). Будем считать, что жидкость движется слева направо, тогда общий для всех ветвей напор в точке А будет больше напора в другой общей для всех ветвей трубопровода точке В (НА
доступных местах (переход через реки и др.). При параллельном соединении трубопроводов имеются две особые точки, называемые точками разветвления. В этих точках находятся концы параллельных ветвей трубопровода (точки А и В). Будем считать, что жидкость движется слева направо, тогда общий для всех ветвей напор в точке А будет больше напора в другой общей для всех ветвей трубопровода точке В (НА  Н к ). В точке А поток жидкости растекается по параллельным ветвям, а в точке В вновь собирается в единый трубопровод. Каждая ветвь может иметь различные геометрические размеры: диаметр и протяжённость (длину). Поскольку вся система трубопроводов является закрытой, то поток жидкости в данной системе будет транзитным, т.е.
Н к ). В точке А поток жидкости растекается по параллельным ветвям, а в точке В вновь собирается в единый трубопровод. Каждая ветвь может иметь различные геометрические размеры: диаметр и протяжённость (длину). Поскольку вся система трубопроводов является закрытой, то поток жидкости в данной системе будет транзитным, т.е.
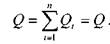
Жидкость движется по всем ветвям при одинаковой разности напоров:
 > тогда расход жидкости по каждой ветви можно записать в виде:
> тогда расход жидкости по каждой ветви можно записать в виде:
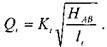
Поскольку ветвей в системе п,, а число неизвестных в системе уравнений будет п+1, включая напор, затрачиваемый на прохождение жидкости по всем ветвям  , то в качестве дополнительного уравнения в системе будет использовано уравнение неразрывности:
, то в качестве дополнительного уравнения в системе будет использовано уравнение неразрывности:
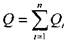
При решении системы уравнений можно воспользоваться соотношением:
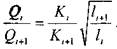
Для построения гидравлической характеристики системы параллельных трубопроводов можно воспользоваться методом графического суммирования. Суммирование осуществляется по  оси расходов Q. т.к.
оси расходов Q. т.к. 
Трубопроводы с непрерывным (распределённым расходом). В данном случае предполагается, что вдоль всей длины трубопровода располагаются одинаковые равномерно
распределённые потребители жидкости. Классическим примером такого трубопровода может служить оросительная система. В начальной точке трубопровода напор составляет Н. В общем случае, расход по трубопроводу состоит из транзитного Qm и расхода Qp ,который непрерывно раз  даётся по всей длине трубопровода.
даётся по всей длине трубопровода.
Тогда в некотором сечении трубопровода на расстоянии х от его начала расход будет равен:
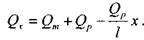
Тогда гидравлический уклон в сечении х на малом отрезке dx:

Уравнение падения напора вдоль элемента dx запишется следующим образом:
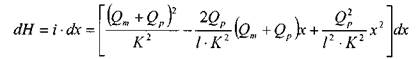
После интегрирования от 0 до / получим:

и при 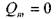 :
: 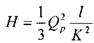
Сети трубопроводов. Если магистральные трубопроводы принято рассматривать как средства внешнего транспорта жидкостей и газов, то сети используются в качестве оборудования для внутреннего транспорта жидких или газообразных продуктов. По направлению движения жидкости (газа) сети различают на сборные и раздаточные (распределительные). В сборных сетях имеется группа источников возникнове  ния жидкости (газа). Жидкость от этих источников направляется в своеобразные узлы сбора и оттуда - в магистральный трубопровод. Классическим примером сборной сети может служить неф-тесборная система со скважин, канализационная сеть. В раздаточных (распределительных) сетях жидкость или газ поступает из магистрального трубопровода и по сети распределяется по потребителям (абонентам). Распространённым приме
ния жидкости (газа). Жидкость от этих источников направляется в своеобразные узлы сбора и оттуда - в магистральный трубопровод. Классическим примером сборной сети может служить неф-тесборная система со скважин, канализационная сеть. В раздаточных (распределительных) сетях жидкость или газ поступает из магистрального трубопровода и по сети распределяется по потребителям (абонентам). Распространённым приме  ром распределительной сети является система водоснабжения. К такому же типу сетей можно также отнести систему принудительной вентиляции,
ром распределительной сети является система водоснабжения. К такому же типу сетей можно также отнести систему принудительной вентиляции,
где воздух подаётся в служебные помещения или на рабочие места. К такому же типу сетей можно отнести систему теплоснабжения и др. Сети строятся в населённых пунктах, на предприятиях, отдельных территориях. Трубы в таких системах могут изготавливаться из различных материалов в зависимости от технологических требований, предъявляемых к сетям. В сборных сетях источники жидкости и газа располагают напором, обеспечивающим движение жидкости (газа) до магистралей. Если напоры недостаточны, то создаются специальные, узлы, где напор обеспечивается принудительным образом. Имеется, по крайней мере, две группы задач для гидравлического расчёта сетей: проектирование новых сетей и расчёт пропускной способности существующих сетей. Принципы расчёта похожи. В основе расчётных формул положены уравнения Дарси-Вейсбаха и Шези. Предварительно в сети выбирается ветвь с наибольшей нагрузкой (расход и напор). Эта ветвь рассматривается как своеобразный трубопровод, который, в общем случае можно отнести к категории последовательного соединения простых трубопроводов. Другие участки рас-
считываются самостоятельно. После завершения расчётных работ, осуществляется проверка соответствия результатов расчётов в узлах сети. После анализа расхождений результатов решений в узлах сети осуществляется корректировка исходных данных. Таким образом, метод итераций является наиболее приемлемым для расчёта сетей.
Трубопроводы некруглого профиля. Подавляющее большинство трубопроводов собирается из круглых труб. Преимущество круглого сечения очевидны: круглое сечение обладает максимальной пропускной способностью и минимальным гидравлическим сопротивлением. Так гидравлический радиус для круглого сечения: 
для треугольного сечения 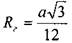 для квадратного сечения
для квадратного сечения 
для шестиугольного сечения 
Тем не менее, трубы некруглого сечения применяются в промышленности там, где потери напора не играют особой роли. Это, в первую очередь, воздуховоды с малыми скоростями движения воздуха, и т.д.
Трубопроводы, работающие под вакуумом (сифоны). Сифоном называется такой самотёчный трубопровод, часть которого располагается выше уровня жидкости в резервуаре. Действующий напор представляет собой разницу уровней в резервуарах Az. Для приведения сифона в действие необходимо предварительно откачать из сифона воздух и создать в нём разряжение. При этом жидкость поднимется из резервуара А до верхней точки сифона, после чего жидкость начнёт двигаться по ниспадающей части трубопровод в резервуар В. Другой ме  тод запуска сифона - заполнить его жидкостью извне. Запишем уравнение Бернулли для двух сечений а-а и b-b относительно плоскости сравнения О - О.
тод запуска сифона - заполнить его жидкостью извне. Запишем уравнение Бернулли для двух сечений а-а и b-b относительно плоскости сравнения О - О.

Поскольку:  , то:
, то:
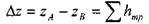 ?
?

Критическим сечением в сифоне будет сечение х - х в верхней точке сифона. Давление в этой точке будет минимальным и для нормальной работы сифона необходимо, чтобы оно выло выше упругости паров перекачиваемой по сифону жидкости.
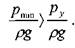
Трубопроводы со стенками из упругого материала. В практике предприятий нефтяной отрасли нередки случаи использования специальных трубопроводов, стенки которых деформируются при изменении давления в перекачиваемой по ним жидкости. К трубопроводам такого типа относятся мягкие и гибкие рукава, резиновые и армированные шланги. Опыты Фримана показали, что в данных случаях можно пользоваться формулой аналогичной формуле Дарси-Вейсбаха:
' > , и 
где; 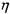 можновзять из таблицы:
можновзять из таблицы:
Характеристика трубопровода Величина rj
Гладкие резиновые рукава 0,000860
Обыкновенные резиновые рукава 0,000899
Очень гладкие, прорезинненые внутри 0,000884
Шероховатые внутри 0,021300
Кожаные 0,013700
Для упругих деформируемых рукавов и шлангов В формулу Дарси-Веёсбаха следует ввести необходимые поправки.

| Характеристика трубопровода | Величина rj | |||
| Гладкие резиновые рукава | 0,000860 | |||
| Обыкновенные резиновые рукава | 0,000899 | |||
| Очень гладкие, прорезинненые внутри | 0,000884 | |||
| Шероховатые внутри | 0,021300 | |||
| Кожаные | 0,013700 | |||
| Для упругих деформируемых рукавов и шлангов В формулу Дарси-Веёсбаха следует ввести необходимые поправки. | ||||
| Номинальный диаметр в мм | Средний внутренний диаметр в мм | 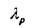
| ||
| При р- lam | Прнр=3ат | |||
| 24,42 | 24,79 | 0,055 | ||
| 31,84 | 32,53 | 0,060 | ||
| 39,84 | 40,80 | 0,080 | ||
| 54,00 | 55,40 | 0,090 | ||
| 65,93 | 67,73 | 0,095 | ||
Дата добавления: 2016-02-20; просмотров: 783;
