Понятие о токе смещения
Для не изменяющегося во времени (стационарного) магнитного поля ротор вектора напряженности равен вектору плотности макроскопического тока:
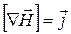 . (20.40)
. (20.40)
Возьмем дивергенцию от обеих частей этого соотношения:
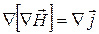 . (20.41)
. (20.41)
С одной стороны, дивергенция ротора всегда равна нулю, с другой - дивергенция вектора плотности тока может быть не равна нулю: в соответствии с уравнением непрерывности
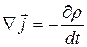 . (20.42)
. (20.42)
Уравнение непрерывности указывает на то, что при нестационарных процессах дивергенция плотности тока может отличаться от нуля. Например, при разряде конденсатора на резистор уменьшающийся заряда на конденсаторе является источником линий вектора плотности тока.
Максвелл предположил, что в правой части уравнения (20.40) ( 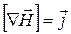 ) в действительности присутствует еще одно слагаемое, т.е. уравнение имеет вид:
) в действительности присутствует еще одно слагаемое, т.е. уравнение имеет вид:
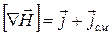 . (20.43)
. (20.43)
Дополнительное слагаемое он назвал плотностью тока смещения.
Определяющим свойством плотности тока смещения является условие .
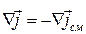 . (20.44)
. (20.44)
Этим обеспечивается выполнение равенства (20.41).
Из уравнения непрерывности следует, что
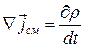 . (20.45)
. (20.45)
Плотность заряда связана с электрической индукцией (электрическим смещением) соотношением:
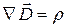 . (20.46)
. (20.46)
Продифференцируем это соотношение по времени и поменяем порядок дифференцирования по времени и координатам:
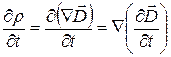 . (20.47)
. (20.47)
Тогда
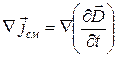 . (20.48)
. (20.48)
Тогда можно утверждать, что
 . (20.49)
. (20.49)
Соответственно ротор напряженности магнитного поля
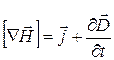 . (20.50)
. (20.50)
Это уравнение является одним из основных в теории электромагнитного поля.
Таким образом, ток смещения по существу представляет собой фактически изменяющееся во времени электрическое поле. Из всех свойств, присущих собственно электрическому току, для тока смещения характерна только одно - способность создавать магнитное поле. Ток смещения присутствует и в обычных проводниках, если в них имеется изменяющееся во времени электрическое поле. Однако в проводниках его плотность пренебрежимо мала по сравнению с плотностью обычного тока.
Дата добавления: 2016-02-11; просмотров: 1535;
