Показатели надежности невосстанавливаемых и восстанавливаемых объектов.
Вероятность безотказной работы объекта - вероятность того, что в определенных условиях эксплуатации в пределах заданной продолжительности работы отказ не возникает. Пусть t - время, в течение которого необходимо определить вероятность безотказной работы, а Т1 - время работы аппаратуры от ее включения до первого отказа. Тогда согласно определению:
P(t)=P (T1³ t),
т.е. вероятность безотказной работы - это вероятность того, что случайная величина T1 (время от момента включения до ее отказа) будет больше или равно времени t, в течение которого определяется вероятность безотказной работы. Функция P(t) является монотонно убывающей функцией времени и при t=0 P(t)=1 (в момент включения объект всегда работоспособен), тогда как P(¥)=0 (объект не может сохранять свою работоспособность неограниченно долго).
На практике иногда более удобной характеристикой является вероятность неисправной работы, или вероятность отказов. Исправная работа и отказ являются события несовместимыми и противоположными. Поэтому вероятность отказа и вероятность безотказной работы связаны зависимостью:
P(t)= 1- Q(t) или Q(t) =P (T 1£ t),
Таким образом, вероятность отказа является функцией распределения случайной величины T1 - времени работы до отказа, т.е. Q(t)=F(t). Производная от интегральной функции есть дифференциальный закон (плотность) распределения: f(t) =dF(t)/dt.
В качестве показателя надежности неудобно использовать функциональную зависимость, поэтому в технических условиях оговариваются значения функции P(t) при значения t выбираемых из нормированного ряда t=100;500;1000;2000;5000;10000 ч.
По статистическому эксперименту можно определить приближенно, в виде статистической оценки:
где N(t) - кол-во безотказно работающих до момента времени t объектов, при их исходном количестве N0.
Вероятность безотказной работы P(t), как количественная характеристика надежности, обладает следующими достоинствами:
1) характеризует изменение надежности во времени;
2) она входит во многие другие характеристики аппаратуры (например, стоимость изготовления);
3) охватывает большинство факторов, влияющих на надежность, и поэтому достаточно полно характеризует надежность;
4) может быть получена расчетным путем до изготовления системы;
5) является характеристикой как простейших элементов, так и сложных систем.
Это явилось причиной наибольшего распространения этой характеристики, однако она имеет существенные недостатки:
1) характеризует надежность восстанавливаемых систем только до первого отказа;
2) не дает возможности установить будет ли готова система к действию в данный момент;
Эти недостатки позволяют сделать вывод, что вероятность безотказной работы, как, впрочем, и любая другая характеристики, не полностью характеризуют такое свойство как надежность, и поэтому не может быть с ним отождествлена.
Частота отказов - это отношение числа отказавших образцов в единицу времени к числу образов, первоначально установленных на испытание при условии, что отказавшие образцы не восстанавливаются и не заменяются исправными. Согласно определению:
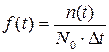
n(t) - число отказавших образцов в интервале времени от t-Dt/2 до t+Dt/2,
N0 - число образцов аппаратуры, первоначально установленных на испытание.
Перейдем от статистического описания частоты отказов к ее вероятностному определению, число отказавших образцов
n(t)= -(N(t+Dt)-N(t)).
При достаточно большом количестве образцов справедливо
N(t)=N0*Р(t),
подставляя в:
Переходя к пределу, при Dt®0 получаем f(t)= -P'(t).
Так как число отказавших образцов в интервале времени Dt может зависеть от расположения этого промежутка по оси времени, то частота отказов является функцией времени и при Dt®0 частота отказов есть плотность распределения времени работы объекта до его отказа: f(t)=Q'(t).
Частота отказов, являясь плотностью распределения, наиболее полно характеризует такое случайное явление, как время возникновения отказов. Вероятность безотказной работы, математическое ожидание и дисперсияявляются лишь удобными характеристиками распределения и всегда могут быть получены, если известна частота отказов f(t).
Эта характеристика имеет существенный недостаток, состоящий в том, что частоту отказов можно использовать для оценки надежности только той аппаратуры, которая после отказа не ремонтируется и в дальнейшем не эксплуатируется (т.е. невосстанавливаемой). Для того чтобы оценить с помощью частоты отказов надежность аппаратуры длительного пользования, которая может ремонтироваться (восстанавливаемых объектов) необходимо иметь семейство кривых f(t), полученных до первого отказа, между первым и вторым, вторым и третьи отказами т.д. Однако следует заметить, что при отсутствии старения указанные характеристики будут совпадать. Частота отказов для восстанавливаемых объектов называется средней частотой отказов или параметром потока отказов и обозначается w(t).
Средней частотой отказов называется отношение числа отказавших образцов в единицу времени к числу испытываемых образцов при условии, что все образцы, вышедшие из строя, заменяются исправными (новыми или восстановленными):
w(t)=n(t)/(N0*Dt).
И соответственно при Dt®0 параметр потока отказов w(t) - это плотность вероятности возникновения отказа восстанавливаемого объекта, определенная для рассматриваемого момента времени. Средняя частота отказов может быть выражена через вероятность безотказной работы:
Эта формула позволяет найти среднюю частоту отказов аппаратуры, если известна ее частота, либо вероятность безотказной работы. Однако на практике найти аналитическое решение это интегрального выражения не всегда удается и приходится применять методы численного интегрирования.
Средняя частота отказов обладает следующими важными свойствами:
1) w(t)³ f(t);
2) независимо от вида f(t) при t®¥ параметр потока отказов стремится к некоторой постоянной величине.
Главное достоинство средней частоты отказов как количественной характеристики надежности состоит в том, что она позволяет довольно полно оценить свойства аппаратуры, работающей в режиме смены элементов, а также надежности при хранении. Она также позволяет определить число отказавших в аппаратуре элементов данного типа.
Интенсивность отказов - отношение числа отказавших образцов аппаратуры в единицу времени к среднему числу образцов .исправно работающих в данный отрезок времени при условии, что отказавшие образцы не восстанавливаются и не заменяются исправными:
Это выражение является статистическим определением интенсивности, от которого также можно прейти к вероятностному:
учитывая, что Nср=N0-n(t), найдем
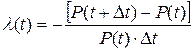, устремляя Dt®0 и переходя к пределу, получим 
для определения учтено (f(t)=Q'(t)=-P'(t))
Интенсивность отказов - условная плотность вероятности возникновения отказа при условии, что до рассматриваемого момента времени отказ не возник:
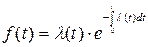и 
устанавливает зависимость между частотой и интенсивность отказов.
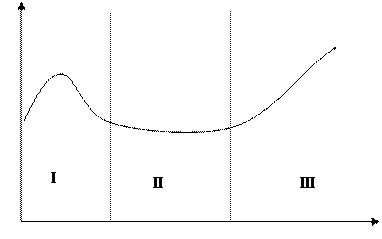Интенсивность отказов, как количественная характеристика надежности, обладает рядом достоинств. Она является функцией времени и позволяет наглядно установить характерные участки работы аппаратуры. Типичная кривая изменения интенсивности отказов по времени эксплуатации приведена на рис.1. Работа элементов и систем характеризуется тремя этапами. Первый этап, характеризуется пиковым увеличением интенсивности отказов - это отказы из-за ошибок проектирования и производственных дефектов. Эти отказы обычно выявляются на заводских испытаниях изделия до ввода в эксплуатацию. К этой группе отказов можно отнести и эксплуатационные отказы, вызванные слабым знанием правил эксплуатации. Этот участок называется период доводки или приработки объекта. Второй этап - период нормальной эксплуатации - характеризуется пониженным уровнем и примерно постоянной интенсивностью отказов и его протяженность во времени гораздо больше других участков. На третьем этапе частота отказов вновь возрастает за счет наступления старения и износа элементов объекта. Этот период называется периодом старения.
Интенсивность отказов как количественная характеристика надежности имеет тот же недостаток, что и частота отказов: она позволяет охарактеризовать надежность аппаратуры лишь до первого отказа. Она используется, как справочная характеристика надежности простейших элементов (микросхем, разъемов и т.п.) По известной характеристике l(t) наиболее просто определяются остальные количественные показатели надежности.
Средним временем безотказной работы называется математическое ожидание времени безотказной работы.
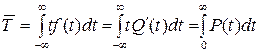
Для определения среднего времени безотказной работы из статистических данных используется: 
, где
ti - время безотказной работы i-го образца,
N0 - число образцов, над которыми проводится испытание.
Основным достоинством среднего времени безотказной работы является его простота вычисления из экспериментальных данных об отказах аппаратуры. Однако характеризует надежность до первого отказа.
У восстанавливаемых объектов, среднее время до первого отказа может существенно отличаться от среднего времени между первым и вторым отказами, вторым и третьим и т.д. Поэтому надежность аппаратуры длительного использования оценивают, в отличии от среднего времени безотказной работы, так называемой наработкой на отказ. Наработкой на отказ называется среднее значение времени между соседними отказами, при условии восстановления каждого отказавшего элемента.
Связь среднего времени между соседними отказами с другими количественными характеристиками надежности проще всего найти через среднюю частоты отказов (параметр потока отказов). Если известны средние частоты отказов элементов сложной системы, то среднее число отказов системы в любом промежутке времени определяется ее суммарной частотой отказов. Тогда среднее время между отказами будет равно величине, обратной суммарной частоте отказов:
(*)
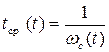При t®¥ среднее время между соседними отказами системы стремиться к ее среднему времени безотказной работы и в пределе равно T.
Время безотказной работы есть наработка до отказа. Тогда как среднее значение времени между соседними отказами есть наработка на отказ. Возможны случаи, когда две совершенно различные функции вероятностей безотказной работы могут давать одинаковые значения средней наработки, и чтобы различить такие случаи применяется среднеквадратическое отклонение наработки до отказа или его квадрат - дисперсия.
Среднее время до отказа является естественным показателем надежности, но не применима в тех случаях, когда:
§ время работы системы гораздо меньше среднего времени безотказной работы;
§ система резервированная;
§ время работы отдельных частей сложной системы разное.
Гамма-процентная наработка tg -наработка, в течение которой гарантируется безотказная работа объекта с заданной вероятностью g.
Таким образом, основными количественными характеристиками надежности невосстанавливаемых объектов в процессе эксплуатации являются: вероятность исправной работы, средняя наработка до отказа, частота и интенсивность отказов. А для восстанавливаемых объектов еще и средняя частота отказов, и средняя наработка на отказ.
Вопросы для самоконтроля
1. Перечислите основные свойства функции надежности.
2. Какая связана частотой и вероятность отказа?
3. Как по известной временной зависимости интенсивности отказов определить частоту отказов и вероятность безотказной работы?
4. Как определить среднее время безотказной работы, если известна временная зависимость частоты отказов? Вероятности безотказной работы?
5. Какие показатели надежности называются комплексными, а какие единичными?
6. Какие показатели надежности зависят от времени, а какие являются статичными?
7. Перечислите безразмерные показатели надежности. Приведите примеры размерных показателей и укажите их размерность.
Дата добавления: 2016-02-20; просмотров: 2375;