Эквивалентная схема источника с линией передачи

Схематично и условно процесс измерения мощности СВЧ сигнала можно представить в виде рис.21.3.1, где 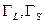– коэффициенты отражения головки и «источника»; последний символизирует цепи, подводящие сигнал к «линии передачи», «мощностная головка» включает сенсор и подает на «измеритель» продетектированный сигнал, «измеритель» может включать оцифровку, регистратор и т. д.

Рассогласование мощностной головки

Линия передачи как двухпортовое устройство, к которому подводится внешняя волна 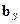измеряемого сигнала и подсоединены «источник» и головка, описывается потоковым графом [21.8], показанным на рис.21.3.2, где 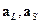– входные, а 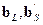– выходные узлы. В условном узле 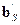суммируются волна 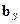и отраженная от «источника» волна, то есть

.

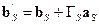(21.3.1)

Нам понадобится также эквивалентная схема с источником эдс (рис.21.3.3), где 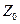– характеристическое сопротивление линии передачи, а 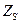учитывает рассогласование источника с этой линией.

Прямая волна в согласованную нагрузку :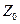

.

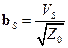(21.3.2)

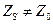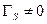Но источник не согласован с линией передачи, поскольку , или . Поэтому

,

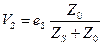(21.2.3)

то есть

.

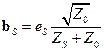(21.3.4)

Согласно теории эквивалентных линий передачи коэффициент отражения от источника:

.

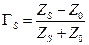(21.3.5)

Мощность, поглощаемая нагрузкой, можно найти как разность между падающей и отраженной мощностями. Из графа рис. 21.3.2 находим падающую волну как:

,

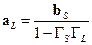(21.3.6)

и отраженную волну как:

.

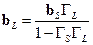(21.3.7)

Разность мощностей этих волн есть поглощаемая в нагрузке мощность:

.

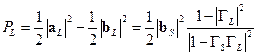(21.3.8)

Как видим, она зависит от двух коэффициентов отражения: 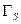и 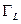. Из этого выражения легко получить известный результат: максимум поглощаемой мощности 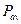по переменной 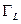достигается при условии сопряженного согласования:

.

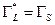(21.3.9)

Подставляя это условие в (21.3.9), получаем:

.

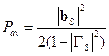(21.3.10)

Потерями сопряженного рассогласования называется [21.16] отношение

,

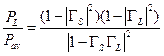(21.3.11)

которое всегда не больше единицы. С другой стороны, если бы нагрузка была согласована с линией передачи, то есть 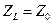и 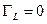, то петля на графе рис. 21.3.2 была разомкнута и, как следует из (21.3.8), было бы

.

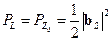(21.3.12)

Потерями 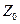-рассогласования называется отношение

,

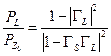(21.3.13)

которое может быть больше единицы; например, при :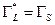

.

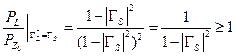(21.3.14)

Неопределенность из-за многократных отражений между генератором и головкой

Предположим, что измеритель мощности идеально зарегистрировал мощность 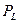, поглощенную чувствительной поверхностью мощностного сенсора. На самом деле, задача заключается в измерении мощности 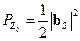, отдаваемой «источником» в согласованную с линией передачи нагрузку, или мощности 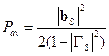, отдаваемой в сопряженно-согласованную с «источником» нагрузку (чаще – первое). Казалось бы, что для пересчета измеренной мощности 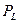в одну или другую названные мощности нужно использовать соотношения (21.3.11) или (21.3.13). Как следует из этих соотношений, для этого нужно знать оба коэффициента отражения: 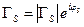и 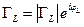, то есть 4 скалярные величины: модули 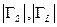и фазы .

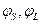Незнание или неполное знание этих величин или некоторых из них является одним из источников ошибки измерения мощности. В отношении информации об этих величин могут быть различные варианты.

1) Неизвестны ни модули, ни фазы коэффициентов отражения 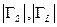. В этом случае пришлось бы полагать знаменатель в правых частях (21.3.11), (21.3.13) равным единице, что привело бы к относительной ошибке оценки мощности, могущей принимать как угодно большое значение. Поэтому данный случай никогда не допускается.

2) Известны только модули 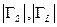, но не фазы коэффициентов отражения. В этом случае диапазон неопределенности оценки знаменателя в правых частях (21.3.11), (21.3.13) дается максимумом и минимумом для худшего случая: 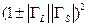[21.16]; это означает, что соответствующая составляющая относительной ошибки оценки мощности принимает значения в примерном диапазоне .

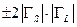3) С некоторыми точностями известны и модули 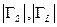, и фазы 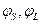(достаточно знать сумму фаз 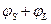), например, в результате исследования цепи детектирования на векторном анализаторе цепей. Тогда соответствующая составляющая ошибки оценки мощности определяется значениями амплитуд и фаз и ошибками их задания.

4) Амплитуды и фазы коэффициентов отражения являются результатом применения скользяще-винтового тюнера [21.16], встроенного в конструкцию головки детектора. Этот вариант редко используется в современных головках, поскольку остаточное отражение от винтов не является незначительным в сравнении с отражением от головки.

5) Модули и фазы коэффициентов отражения неизвестны, но задан так называемый калибровочный коэффициент головки. Этот случай рассмотрен ниже.

Калибровочный коэффициент мощностной головки и кпд

Мощностная головка почти идеально собирает всю мощность, рассеянную на эффективной нагрузке, представленной детекторным элементом и его схемой. Но выше мы уже видели, что несовершенное согласование означает, что только часть 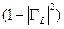падающей мощности поглощается нагрузкой. Однако даже не вся эта часть окончательно достигает детекторного элемента, поскольку имеются некоторые потери в стенках и некоторая часть излучается в пространство, или стекает в проходимые элементы конструкции. К.п.д. мощностной головки 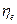, определяемый как отношение собранной мощности на детекторном элементе к полной рассеянной на нагрузке мощности, таким образом, уменьшается (кроме того, как мы видели, отраженная от нагрузки волна, дойдя до «источника», отражается от него, и вливается с некоторой фазой на чувствительную поверхность). Из падающей мощности 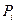часть 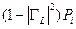не отражается, но только часть поглощается детекторным элементом. Результирующее отношение падающей мощности к поглощенной элементом называется калибровочным коэффициентом 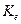, который, таким образом, равен:

.

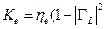(21.3.15)

Производители мощностных головок обычно снабжают их таблицей калибровочных коэффициентов на специальных частотах (эти коэффициенты должны трассироваться до национальных стандартов), и современные мощемеры могут быть установлены корректно как по к.п.д, так и по потерям рассогласования через единственный коэффициент .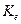

Пусть целью измерения является согласованная мощность 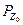, падающую на головку мощность обозначим 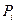, результат измерения до коррекции (кажущаяся мощность) – 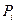. Коррекция с помощью калибровочного коэффициента дает

.

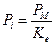(21.3.16)

С другой стороны, с помощью (21.3.6) получаем:

,

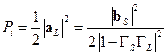(21.3.17)

и подставляя сюда правое равенство (21.3.12), имеем:

.

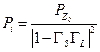(21.3.18)

Сравнивая (21.3.18) с (21.3.16), видим, что даже после применения коррекции к кажущейся мощности 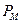с помощью калибровочного коэффициента, лучшей оценкой мощности 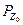является величина 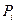, полученная по (21.3.16); эта оценка имеет неопределенность в диапазоне худших случаев: 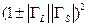, то есть относительная ошибка принимает значения в примерном диапазоне .

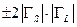Поскольку мы получили те же неопределенность и диапазон относительной ошибки оценки, что и в 21.3.2 2), возникает вопрос: зачем нужно знать и применять калибровочный коэффициент 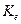? Ответ состоит в том, что знание 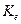, определяемого заводом-изготовителем мощностной головки, избавляет пользователя от необходимости проведения непростого калибровочного определения модулей 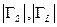коэффициентов отражения.