Уравнение бегущей волны. Если молекулы, из которых состоит среда, взаимодействуют, то колебания молекул могут распространяться в среде

ВОЛНОВЫЕ ПРОЦЕССЫ

Основные понятия

Если молекулы, из которых состоит среда, взаимодействуют, то колебания молекул могут распространяться в среде. Когда одна молекула смещается из положения равновесия, она оказывает влияние на соседние молекулы. В итоге они также смещаются. Поскольку твердое тело может состоять из атомов, которые также участвуют в колебательном процессе, будем говорить о частичках среды, не конкретизируя их природу. Движение частиц в среде – это колебательный процесс. С течением времени в него вовлекаются частички, отстоящие все дальше от источника возбуждения. Таким образом, возбуждение в среде передается с конечной скоростью, и этот процесс называется волновым. Частички, которые участвуют в этом процессе, колеблются с различными фазами. Если силы взаимодействия упругие, то процесс протекает без потери энергии. Распространение колебаний – это распространение волны. Волна переносит энергию, но частицы остаются на месте, совершая колебательные движения. Нет переноса вещества. Волны могут быть поверхностными, объемными, упругими. Упругие волны могут быть продольными и поперечными. Такая классификация связана с тем, как смещаются частички относительно направления распространения волны. Когда они совпадают, такие волны называются продольными. Продольные волны возникают при деформации сжатия и растяжения. Средой служит газ, жидкость, твердое тело. Поперечные волны возникают при деформации сдвига и существуют только в твердых телах. Упругая волна называется гармонической, если колебания частиц в ней являются гармоническими. Распространение колебаний – это волновой процесс.

Рис

Пусть 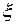- смещение частичек среды. Смещение частиц в волне 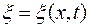. Если зафиксировать 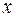, то функция будет описывать колебания частиц. Если взять ближайшие частицы, которые колеблются в одинаковой фазе, то расстояние между ними определяет длину волны. Все частицы, расстояние между которыми кратно целому числу длин волн, колеблются в одинаковой фазе. Если волна распространяется со скоростью 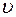, то

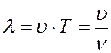и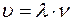

где 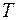- период колебаний, 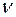- частота колебаний. Геометрическое место точек, до которого доходят колебания к моменту времени 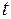, называется волновым фронтом. Геометрическое место точек, которые колеблются в одинаковой фазе, называется волновой поверхностью. Если волновая поверхность – плоскость, то волна называется плоской. Если волновая поверхность – сфера, то волна называется сферической.

Уравнение бегущей волны

Бегущей волной называется волна, которая переносит в пространстве энергию. Перенос энергии характеризуется вектором плотности потока энергии. Для упругих волн этот вектор называется вектором Умова. Плотность потока энергии – это поток энергии в единицу времени через единичную площадку, причем направление распространения волны совпадает с нормалью к площадке. Найдем уравнение бегущей волны. Пусть в среде вдоль оси 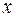распространяется упругая волна со скоростью 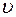. Источник находится в точке 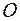. Там же находится начало координат. Источник совершает гармонические колебания (частицы, совершающие колебания в плоскости ).

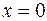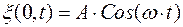
Колебания частиц среды, находящихся в точке, отстоящей на расстоянии 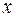, будут отставать на времени 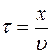. Тогда уравнение колебаний частиц, лежащих в плоскости 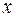имеет вид

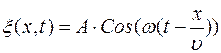(1)

Отсюда замечаем, что 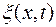- периодическая функция времени и координаты. Ур.(1) – это уравнение бегущей волны. Если учесть начальную фазу, то уравнение бегущей волны примет вид

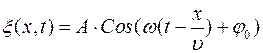(2)

Величина

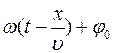
называется фазой бегущей волны. Для описания волны используется волновое число

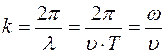(3)

Тогда фазу волны можно записать в виде

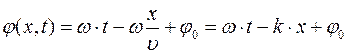(4)

Уравнение бегущей волны

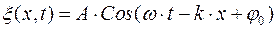(5)

или

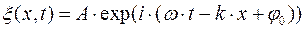(6)

Волна распространяется в положительном направлении 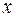. Если волна распространяется в отрицательном направлении 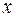, то 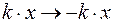. Пусть фаза постоянная

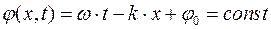
найдем дифференциал фазы

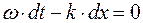. Отсюда

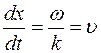(7)

Скорость, которая определяется формулой (7), называется фазовой скоростью. Эта скорость – скорость перемещения фазы волны. Если фазовая скорость зависит от частоты, то это явление называется дисперсией волн. Если при распространении волны в среде, свойства среды не изменяются, то такая среда называется линейной. Для линейной среды справедлив принцип суперпозиции: при распространении нескольких волн, каждая из них распространяется независимо от остальных. Результирующее колебание есть векторная сумма отдельных колебаний.

Рассмотрим волновой пакет - суперпозицию волн, которые мало отличаются по частоте и занимают ограниченную область пространства в любой момент времени. Для простоты рассмотрим две волны с одинаковыми амплитудами и близкими частотами, что эквивалентно 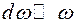и 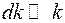. Тогда суммарная амплитуда

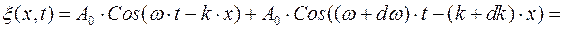
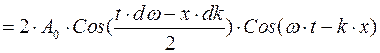(8)

Эту волну можно рассматривать как гармоническую с амплитудой

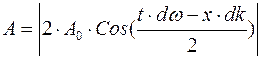(9)

Амплитуда медленно изменяется с 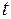и 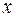. За скорость распространения волнового пакета (8) принимают скорость перемещения максимума амплитуды волны. Максимум амплитуды находится из условия 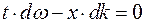отсюда 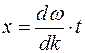. Величина

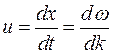(10)

называется групповой скоростью. Найдем связь между групповой и фазовой скоростями.

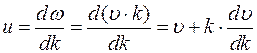
Учтем, что 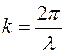отсюда 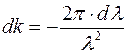. Подставим в групповую скорость

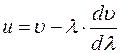(11)

Если 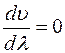, то 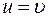совпадают.