Два способа построения сетки из гексаэдров

· В ответ на команду построения сеток из гексаэдров появится диалоговое окно – рис.50.

· Самое первое поле, на которое следует обратить внимание – это поле Тип. В нем присутствуют две опции (рис.51).

· Представьте, что вы собираетесь построить КЭ сетку из гексаэдров для детали, показанной на рис.52. Особенностью этой детали является то, что её исходная и конечная грани для выращивания гексаэдров “состоят из одного куска”. В этом случае можно выбрать первую опцию – Наследованное множественное тело построения. Здесь и во многих иных местах перевод терминов либо неудачен, либо непонятен. С этим часто приходится мириться.

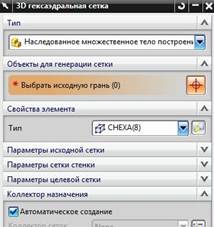
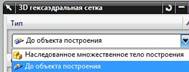
Рис.50 рис.51 рис.52 рис.53

· Следующим шагом вы должны указать курсором лицевую грань (рис.53), и в итоге сетка будет благополучно построена (рис.54).

Рис.54 рис.55 рис.56 рис.57 рис.58

· А если вы начнете строить сетку из гексаэдров для детали, показанной на рис.55, то сразу бросается в глаза, что её лицевая грань состоит из двух кусков, а оборотная сторона – из одного куска. В этом случае вам придется выбрать опцию До объекта построения.

· При этом в верхней части диалогового окна система предложит вам раздельно указать исходную грань, и грани на целевом теле (рис.58).

· Указывая исходную грань, вам придется указать на два её куска (рис.57, 58). Потом вам придется повернуть модель, и указать единственную часть оборотной стороны модели (рис.60, 61). В итоге вы построите сетку из гексаэдров, как это показано на рис.62.

рис.59

· Важно соблюдать именно такую последовательность указания граней тела: сначала ту грань, на которой несколько кусков, а потом грань, состоящую из одного куска. В противном случае система выдаст сообщение об ошибке (рис.59).

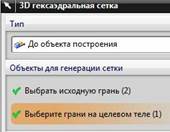
Рис.60 рис.61 рис.62 рис.63

· Вот так, отдельно для каждой части, в итоге вы построите общую сетку детали (рис.63). Может быть, вам покажется такая процедура слишком сложной. Но итоговая сетка окажется более качественной, чем аналогичная сетка из тетраэдров.

· Более того, число гексаэдров (при равной величине) окажется гораздо меньшим, чем число тетраэдров! Чтобы убедиться в этом, вы можете в панели инструментов выбрать команду Информация о конечно – элементной модели (рис.64).

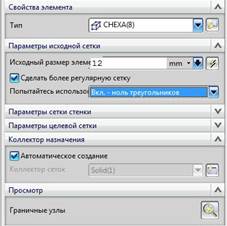
Рис.64 рис.65 рис.66

(Нумерация рисунков в следующем параграфе начинается с цифры 60)