Двухполюсник с потерями.
При Z=R+jX придется рисовать два графика: фазовый и сопротивлений.
Цепи первого порядка (одноэлементный двухполюсник)
| R4 |
| R3 |
| R1 |
| R1 |
| L2 |
| C1 |
| L1 |
| C2 |
Основной характеристикой двухполюсника является частотная характеристика. Частотную характеристик можно представить в двух системах координат: комплексной и полярной системах координат.
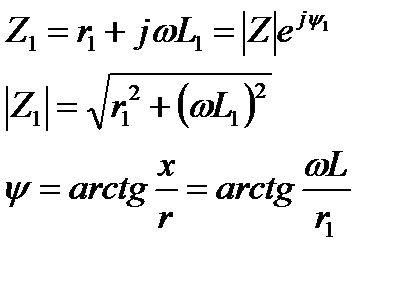(4.24)
; 
;
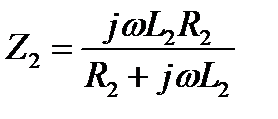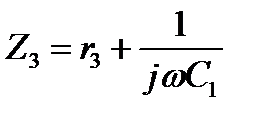
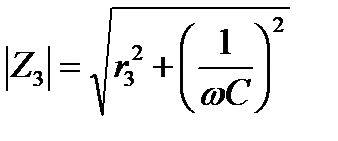
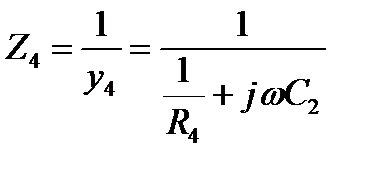
Двухэлементные двухполюсники с потерями.
Здесь возможен резонанс.
r-может быть потерями или непосредственно активное сопротивление, которое напаяны в схему.
Ζ1=r+j (ωL –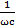 
)
Z=√r2+(ωL –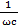 
) 2
Z=arctg ωL- 
Z1
w
wрез.
Резонанс Zm(Z1)=0
ωрез1=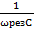 
ωрез = 
2)
Y2=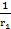 
+jωL+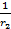 
+ 
= 
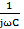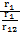+ω2L2+ 
+ 
+ω2L2+ + 
=Re(Y2)
Ym (Y2)=-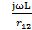 
+ωрез2L2 + 
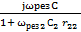= 0
-L-ωрез2C2 L r22+ r12C+ ωрез2L2 C=0
ωрез= 
= 
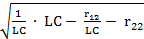
резонанс возможен в следующей ситуации
4 C> r12 4 C> r12
L/C> r22 L/C> r22
L/C > r12 L/C> r12
L/C< r22 L/C< r22
Вывод: таким образом в параллельном контуре с потерями
1) Не всегда есть резонанс токов
2) Резонансная частота зависит не только от величин активных сопротивлений, но и от сопротивления потерь r(R)
3) Часто используют контура с очень малыми потерями
4) 4 C>> r12 (r22) ωрез =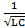 
Но стабильность настройки контура (неизменность резонансной частоты) зависит не только от стабильности L и C, но и от стабильности потерь r1, r2.Поэтому в цепях (схемах), где нужно иметь очень стабильную частоту, контур определяющий стабильность работы устройств не должен непосредственно нагружаться, а нагрузка включается через каскад.
| f |
| π/2 |
| π/2 |
| Ψ |
| Ψ |
| |Z2| |
| f |
| Ψ1 |
| R1 |
| |Z1| |
| f |
| f |
| Ψ2 |
| R2 |
| f |
| -π/2 |
| Ψ |
| |Z3| |
| Ψ3 |
| R3 |
| f |
| f |
| -π/2 |
| Ψ |
| |Z4| |
| Ψ4 |
| R4 |
| f |
Дата добавления: 2015-12-08; просмотров: 1344;