Частотные характеристики пассивных двухполюсников

Как выяснили выше, входное сопротивление и входная проводимость двухполюсника являются функциями частоты ω. Под частотными характеристиками (ЧХ) понимают следующие типы характеристик:

1. Зависимость модуля входного сопротивления (проводимости) от частоты ω.

2. Зависимость действительной или мнимой части входного сопротивления (проводимости) от частоты ω.

ЧХ могут быть получены расчетным (если известна схема, характер элементов и их числовые значения), либо опытным путем (в этом случае схему двухполюсника и характер её элементов знать не обязательно).

При снятии ЧХ опытным путём на вход двухполюсника подают напряжение, частоту которого изменяют в широких пределах, начиная с нуля, и по результатам измерений подсчитывают модуль входного сопротивления (проводимости) или действительную (мнимую) часть входного сопротивления (проводимости).

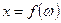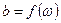В общем случае двухполюсники содержат резистивные и реактивные элементы. В частном случае двухполюсники могут состоять из реактивных элементов, тогда их называют реактивными двухполюсниками. Применительно к ним под ЧХ понимают зависимости или . ЧХ для несложных двухполюсников, содержащих резистивные и реактивные элементы, иногда можно качественно строить на основании простых физических изображений о характере изменения сопротивления отдельных элементов этого двухполюсника при изменении частоты. Если это сделать затруднительно, то прибегают к аналитическому расчету, либо к снятию ЧХ опытным путём.

Рассмотрим вопрос о построении ЧХ реактивных двухполюсников, не содержащих резистивных сопротивлений.

Входное сопротивление их 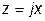, а входная проводимость .

Частотная характеристика таких двухполюсников - это зависимость 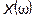или 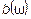. Эти зависимости взаимно обратные.

Для индуктивного элемента (рис. 3.25а), а проводимость 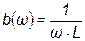(рис. 3.25б). Для емкостного элемента (рис. 3.25в), а 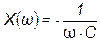(рис. 3.25г). Если учесть, что при последовательном соединении элементов их сопротивления складывают, то ясно, что для получения последовательно соединенных элементов надо сложить ординаты кривых этих элементов.

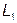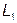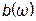ЧХ последовательно соединённых и (рис. 3.25д) построена на рис. 3.25е в виде кривой 3 (прямая 1 – это ЧХ , а кривая 2 – ЧХ ). Зависимость для схемы (рис. 3.25 д) изображена на рис. 3.25ж. При частоте 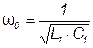кривая пересекает ось абсцисс, а кривая 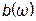претерпевает разрыв от 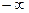до . При этой частоте имеет место резонанс напряжений.

Если учесть, что при параллельном соединении элементов проводимости их надо сложить, то для получения кривой 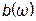параллельно соединённых элементов надо сложить ординаты кривых 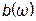этих элементов. Зависимость 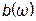для схемы на рис. 3.25з изображена на рис. 3.25к, а обратная ей зависимость - на рис. 3.25и.

При частоте кривая 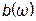пересекает ось абсцисс, а претерпевает разрыв от до 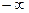. При этой частоте имеет место резонанс токов. На рис. 3.25л последовательно соединены два двухэлементных двухполюсника. Так как каждого из этих двухполюсников построена, то результирующее схемы на рис. 3.25л получим, суммируя ординаты этих двухполюсников. Зависимость изображена на рис. 3.25м, а 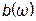- на рис. 3.25н. При плавном увеличении частоты в схеме на рис. 3.25ж начиная с 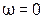при частоте 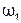возникает резонанс напряжений, затем при частоте - резонанс токов, после этого снова - резонанс напряжений при частоте . При дальнейшем увеличении резонанс возникать не будет.

Сделаем следующие выводы:

1. Режимы резонанса токов и резонанса напряжений чередуются (рис. 3.25л).

2. Число резонансных частот для канонических схем на единицу меньше числа реактивных элементов.

3. Если в схеме есть путь для прохождения постоянного тока, то при плавном увеличении частоты, начиная с нуля, первым наступит резонанс токов, если нет – резонанс напряжений.