Свойства функций реактивных двухполюсников
Исследование функций Z и Y проводят с использованием следующих свойств:
1. Общее число нулей и полюсов на единицу больше числа элементов, число резонансов на единицу меньше числа элементов. В число нулей и полюсов входят и резонансы.
Число резонансов на единицу меньше числа элементов.
2. Нули и полюса функции Z , Y строго чередуются.
3. Функции Z, Y могут иметь асимптоты: вертикальную ось, горизонтальные асимптоты, наклонные асимптоты типа jωLэ.
4. dZ /dw ≥ 0 ( dy/dw ≥ 0 ) , т.е функции Z и Y возрастающие.
Производная по частоте от сопротивления положительна.
Реактивные двухполюсники различают по числу элементов

≡
LЭ = 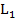 +
+ 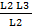 +
+ 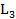
Основной характеристикой двухполюсника является частотная характеристика сопротивления или частотная характеристика проводимости
Ζ(jω)= 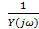
Рассмотрим простейшие двухполюсники и их частотная характеристика:
1.
Ζ1=jωL1
График зависимости сопротивления этого одноэлементного двухполюсника от частоты
2.
Ζ2=
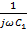
График зависимости сопротивления от частоты
Формула Фостора
позволяет записать аналитическое выражение Z двухполюсника без вывода
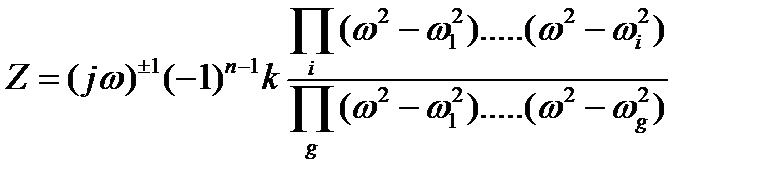 (4.3)
(4.3)
Количество скобок столько сколько резонансов напряжений ( в числители ).
Количество скобок в знаменатели равно числу резонансов токов.
+1 - если схема пропускает постоянный ток
– 1 - если схема пропускает постоянный ток
n - 1 число резонансов
k- определяется из поведения двухполюсника при стремлении w→∞.
| C6 |
| 1. |
| C1 |
| L1 |
| L2 |
| K1=L2 |
| 2. |
| C2 |
| L3 |
| L4 |
| K2=Lэ |
| 3. |
| C3 |
| L5 |
| C4 |
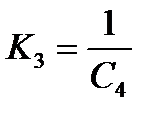
|
| L6 |
| 4. |
| C5 |
| K4=C5+C6/C5C6 |
К - коэффициент определяется из поведения двухполюсника при ω = ∞ путем замыкания С или разрыва индуктивностей L, но так , чтобы оставалась цепь между зажимами двухполюсника «К» может быть двух видов.
K=Lэ 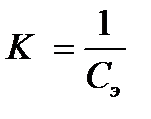
ПРИМЕР:
1) n=3
При ω→∞ остается только С5, т.к при ω→∞ ZL4=jωL4→∞ И ТОК ПОТЕЧЕТ ПО ПУТИ С5, ТОГДА
К 5= 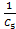
2)
Т.к при ω→∞ ХC= 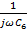 →0,то схема будет иметь вид (при ω→∞)
→0,то схема будет иметь вид (при ω→∞)
или
LЭ = 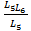 + L6 и K6 = LЭ =
+ L6 и K6 = LЭ = 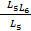 + L6
+ L6
3)
При ω→∞ схема будет иметь вид, т.к ток течет по пути наименьшего сопротивления, а при ω→∞
XL = jωL →∞, тогда
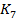 =
= 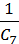
В соответствие с формулой Фостера выражения для Z двухполюсников 1 - 4 примут вид :
Ζ1 = 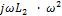 -
- 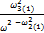
Ζ2 = j 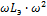 -
- 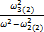
Ζ3 = 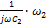 -
- 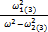
Ζ4 = 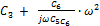 -
- 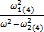
Дата добавления: 2015-12-08; просмотров: 778;
