УРАВНЕНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ

ЭЛЕКТРОПРИВОДА

В работе электропривода различают два основных режима: установившийся и переходный. В установившемся режиме электропривод работает с постоянной скоростью. Нарушение постоянства скорости (при регулировании хода технологического процесса, изменении параметров питающего напряжения и др.) вызывает переходный режим, в течение которого система «электродвигатель – рабочая машина» переходит в новое установившееся состояние.

Изучением поведения электропривода в переходных режимах занимается динамика электропривода, используя уравнение движения электропривода. Рассмотрим данное уравнение. При работе электропривода под нагрузкой с постоянной скоростью вращения вращающий момент электродвигателя М уравновешивается статическим моментом сопротивления М_с, приложенным к валу электродвигателя со стороны рабочей машины, т.е.

М = М_с. (4.1)

Такой режим работы электропривода называется установившимся. При нарушении равенства (4.1) возникает динамический момент М_дин, характеризующий переходный режим. При этом уравнение равновесия моментов имеет вид

М = М_с + М_дин, (4.2)

где М – вращающий момент электродвигателя, Н∙м;

М_с – статический момент сопротивления, приведенный к валу электродвигателя, Н∙м;

М_дин – динамический момент, приведенный к валу электродвигателя, Н∙м.

Рассмотрим подробнее отдельные составляющие уравнения (4.2). Вращающий (или электромагнитный) момент электродвигателя М создается в результате взаимодействия магнитного потока с током, протекающим по ротору или якорю электродвигателя. Момент на валу электродвигателя М_в отличается от электромагнитного момента М на величину момента потерь холостого хода М₀, определяемого трением в подшипниках, щеток о коллектор или кольца, вентиляторными потерями и потерями в стали. Момент на валу электродвигателя зависит от режима работы электропривода. В двигательном режиме момент М₀ уменьшает момент на валу, а в тормозном режиме увеличивает его. Поэтому

М_в = М ± М₀.

Величина М₀ составляет несколько процентов от номинального момента М_н на валу электродвигателя.

Вращающий момент электродвигателя считается положительным, если он направлен в сторону движения рабочей машины, и отрицательным – если против движения (режим торможения).

Момент статического сопротивления М_с состоит из момента полезной работы (например, подъем груза) и момента трения М_тр, который учитывается коэффициентом полезного действия механизма.

Моменты, соответствующие полезной работе, бывают двух видов: реактивные и активные.

Реактивные моменты – это моменты, которые во всех случаях являются тормозящими, противодействующими движению.К ним относятся моменты резания, кручения, давления, сжатия неупругих тел и моменты трения. Реактивные моменты меняют свой знак при изменении направления вращения привода.

Активные (или потенциальные) моменты – это моменты от веса, сжатия, растяжения и скручивания упругих тел. В отличие от реактивных активные моменты сохраняют направление своего действия при изменении направления вращения привода. Они могут быть направлены как по направлению движения, так и против него. Активные моменты, препятствующие движению, принимаются со знаком «минус», а способствующие движению – со знаком «плюс».

Динамический момент определяется угловым ускорением (замедлением) и моментом инерции системы электропривода:

М_дин = J ,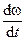

где J – момент инерции всех движущихся частей, кг∙м²;

dω/dt – угловое ускорение (замедление), рад/с²;

ω – угловая скорость, рад/с;

t – время, с.

При постоянном моменте инерции уравнение движения электропривода (4.2)

М = М_с + J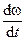

или М – М_с = J 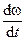. (4.3)

Знак перед М_дин, а следовательно, и перед dω/dt зависит от соотношения величин и знаков М иМ_с. При М > М_с привод ускоряется, dω/dt > 0, М_дин – положительная величина. При М <М_с привод замедляется, dω/dt < 0, М_дин – отрицательная величина. Когда М = М_с, ускорение или замедление отсутствует, т.е. dω/dt = 0, М_дин = 0, привод работает в установившемся режиме с постоянной скоростью ω.

В общем виде уравнение движения электропривода (4.3) с учетом режимов работы электродвигателя и знаков моментов можно записать

± М ± М_с = J .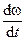

Время разгона и торможения электропривода.Время переходного режима для некоторых производственных механизмов в значительной степени определяет их производительность, влияет на выбор электродвигателя и т.д.

Для определения времени переходного процесса необходимо решить уравнение движения электропривода относительно времени:

dt = J dω /(М – М_с),

откуда t = ∫ J dω / (М – М_с).

Для решения данного уравнения необходимо знать зависимости момента двигателя М и момента сопротивления М_с от угловой скорости ω. Частные случаи этой задачи должны учитывать знаки моментов и пределы интегрирования.

При разгоне электродвигателя с помощью пускового реостата можно принять момент электродвигателя постоянным и равным:

М = αМ_н = const,

где αМ_н – средний момент при пуске;

α – коэффициент, учитывающий кратность среднего пускового момента по отношению к номинальному моменту электродвигателя М_н.

Для случая пуска электродвигателя из неподвижного состояния с М_с = const и J = const время разгона

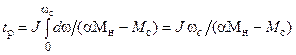. (4.4)

При электрическом торможении электропривода уравнение движения будет иметь вид

– М – М_с = J (dω/dt).

Из этого уравнения следует, что время торможения электропривода

.

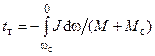Принимая по-прежнему М = α М_н = const, М_с =const, J = const, время торможения от скорости ω_с до 0 будет

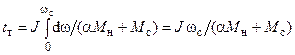. (4.5)

Анализ полученных выражений для t_р и t_т показывает, что одним из существенных факторов, определяющих длительность переходного процесса, является момент инерции электропривода. Поэтому в электроприводах с частыми пусками и торможениями применяют специальные электродвигатели с уменьшенным диаметром при соответствующем удлинении ротора (крановые электродвигатели). В электроприводах большой мощности вместо одного двигателя устанавливают два – каждый половинной мощности, что позволяет сократить время переходного режима в два раза.

Выбор оптимального передаточного числа редуктора.При проектировании и модернизации электропривода приходится решать задачу по выбору оптимального (наивыгоднейшего) передаточного числа редуктора i_опт. Практически это сводится к определению номинальной скорости вращения электродвигателя. Если электродвигатели одинаковой мощности, но с большей номинальной скоростью имеют меньшие габариты, массу и стоимость, то целесообразно использовать более быстроходные электродвигатели. Однако при этом оказывается, что редуктор должен иметь большее передаточное число (это повышает его стоимость). Для электроприводов с редкими пусками выбор i_опт (или номинальной скорости вращения электродвигателя) производится из условия наименьшей общей стоимости электродвигателя и редуктора.

Для электроприводов с частыми пусками наиболее существенным критерием является сокращение общего времени переходного процесса t_р + t_т до минимума. Рассмотрим определение i_опт, исходя из минимума времени переходного процесса t_п.п. Представим время переходного процесса, используя выражения (4.4) и (4.5), в таком виде:

t_п.п = t_р + t_т = (J_дδ + J_м / i²) ω_с / (α М_н – М_с) + (J_дδ + J_м / i²) ω_с / (α М_н + М_с). (4.6)

Здесь суммарный момент инерции системы электропривода J, приведенный к валу электродвигателя, представлен в виде

J = J_дδ + J_м / i²,

где δ = 1,1…1,3 – коэффициент, учитывающий момент инерции редуктора (так как момент инерции редуктора в большинстве своем неизвестен, то его в расчетах принимают равным 10…30 % от момента инерции ротора электродвигателя I_д), т.е. составляющая J_дδ – это суммарный момент инерции ротора электродвигателя и редуктора.

Принимая ω_с =ω_н, умножим и разделим оба слагаемых выражения (4.6) на ω_н и учтем, что

М_н ω_н = Р_н; М_с ω_н = Р_с; J_дδ ω_н² = 2W_к.д;

J_м (ω_н / i)² = J_м ω_м² = 2W_к.м.

Здесь ω_н – номинальная угловая скорость вращения.

Тогда

t_п.п = 2 (W_к.д + W_к.м) / (α Р_н – Р_с) + 2(W_к.д + W_к.м) / (α Р_н + Р_с), (4.7)

где W_к.д – кинетическая энергия ротора электродвигателя с редук-тором;

W_к.м – кинетическая энергия движущихся частей механизма;

Р_н – номинальная мощность электродвигателя;

Р_с – статическая мощность нагрузки на валу электродвигателя.

Номинальная мощность электродвигателя определяется его нагревом при данной нагрузке и является неизменной величиной. Статическая мощность нагрузки определяется работой, которую должен совершить исполнительный механизм. Кинетическая энергия механизма определяется его конструкцией. Следовательно, единственной величиной, которую можно изменять в (4.7), является кинетическая энергия W_к.д. При минимуме W_к.д будем иметь минимум времени переходного процесса t_п.п. 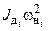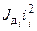Отсюда следует простое правило определения оптимального передаточного числа редуктора: для заданной номинальной мощности Р_н из каталога выбирают несколько электродвигателей на разные номинальные скорости и вычисляют произведение (или , так как 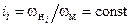), из которых выбирают наименьшее.

Тогда

i_опт = ω_{н опт} / ω_м.