Способы получения булевых случайных величин
1. Равновероятностный двоичный элемент - триггер с включением и выключением питания.
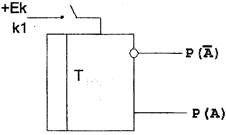
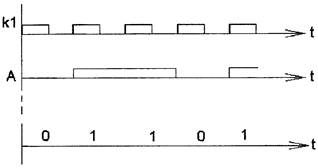
P(A) = p; P(B)=q; p=l-q
Необходимое условие: симметричность
коррекция вероятностей
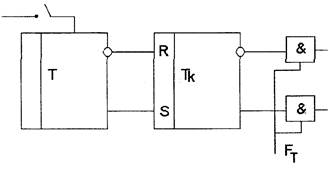
Найдем вероятность перехода за 1 шаг (Для триггера Тк)

Пусть р=0.4, т.е. отклонение = 0.1, тогда уже для двух шагов:
Р00 = 0.52
P01 = 0.48
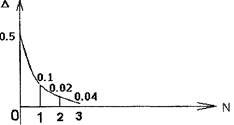
т.е. отклонение составит Δ = 0.02. Был проведен математический анализ, показавший, что 1) Δ = 0.5(1-2p)N, Где N - количество шагов. Для нашего случая N=2, р=0.4 Δ = 0.02, т.е. с увеличением N отклонение от равной вероятности уменьшается.
2) Задаваясь величиной отклонения 0.05, можно найти то N, при котором будет выполняться заданное отклонение. Однако этот способ получения булевых случайных величин приводит к уменьшению быстродействия в N раз.
2. Вероятностный двоичный элемент с управляемой вероятностью.
Пусть имеется двоичное разложение какого-то числа, например, 0.75 = 0,1100 Имеются независимые булевые случайные величины с вероятностью равной 0.5. Используя коньюнктор, можно получить б.с.в. с вероятностями, равными 0.25, 0.125 и т.д. Используя дизъюнктор, можно производить суммирование б.с.в. получая суммы вероятностей. Для данного примера вероятность равна 0.5 + 0.25, что в логической схеме реализуется с помощью дизъюнктора:
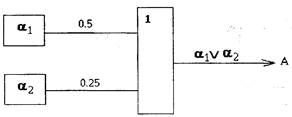
Примечание: α1, α2 - несовместные б.с.в. Обобщаем эту схему:
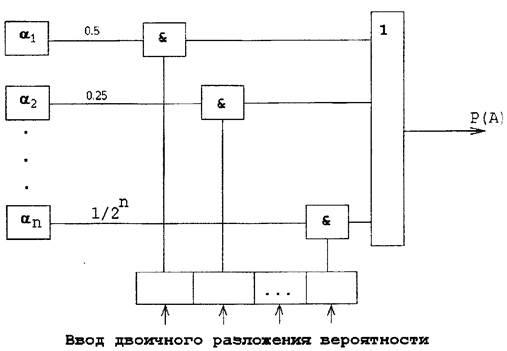
Дата добавления: 2016-02-09; просмотров: 782;
