ТРЕТИЙ ЗАКОН ТЕРМОДИНАМИКИ

Протекание химических реакций связано с изменением со­стояния атомов в молекулах реагирующих веществ. При этом происходит изменение внутренней энергии, которое может проявляться в виде выделяющейся теплоты реакции и различных работ:

ΔU = Q – L – A,

где Q - теплота реакции; L = _V1∫^V2 р dV - работа изменения объема (против внешних сил); А - сумма работ против электрических, световых, магнитных, звуковых и других сил, проявляющихся в ходе химической реакции и сопутствующих воздействий.

Уравнение первого закона термодинамики, выраженное че­рез энтальпию, можно представить в виде

ΔI = Q + _p1∫^p2Vdp – A

Рассмотрим процессы, когда фиксированными являются два параметра: (v, Т) = const или (р, Т) = const.

Для процесса при (v, Т) = const уравнение запишется в виде

ΔU_v,T = Q_v,T – A_v,T

или

A_v,T = Q_v,T – ΔU_v,T (*)

Для процесса при (р, Т) = const уравнение будет иметь вид

ΔI_p,T = Q_p,T – A_p,T

или

A_p,T = Q_p,T – ΔI_p,T (**)

В приведенных уравнениях изменения внутренней энергии и энтальпии происходят за счёт отвода теплоты реакции и совершения работы против внешних сил.

Выражая теплоту через изменение энтропии в виде Q = T(S₂ – S₁) и учитывая, что

F = U – TS, – изохорно-изотермический потенциал или свободная энергия Гельмгольца (мера работоспособности системы)

G = I – TS, – изобарно-изотермический потенциал или свободная энергия Гиббса (определяет наличие обратимых и/или необратимых процессов в системе)

уравнения (*) и (**) перепишутся в виде

A_v,T = (F₁ – F₂)_v,T A_p,T = (G₁ – G₂)_p,T

Дифференцируя F = U – TS, получаем

dF = dU – TdS – SdT.

Учитывая, что в обратимых процессах

TdS = dU + pdV или dU – TdS = – pdV,

получаем dF = –SdT – pdV.

Продифференцируем это уравнение по Т при V = const.

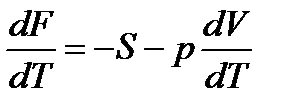
Уравнение превращается в частную производную и принимает вид

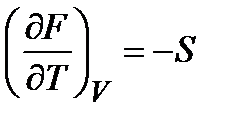, откуда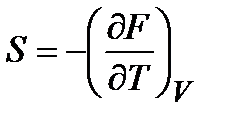

Следовательно:

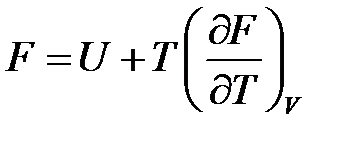
При переходе термодинамической системы из одного со­стояния в другое в обратимом химическом процессе при (v, Т) = const совершается максимальная работа

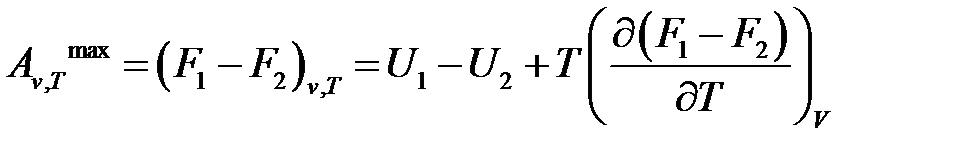
При записи теплового эффекта (максимальной выделяемой или поглощаемой теплоты) химической реакции в виде

Q_V = (U₂ – U₁)_v,T

получаем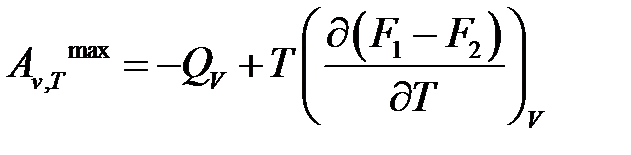

Аналогично, если рассмотреть химическую реакцию в ус­ловиях термодинамической обратимости, протекающую в изобарно-изотермической термодинамической системе при (р, Т) = const, получим

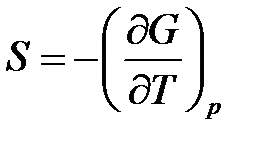
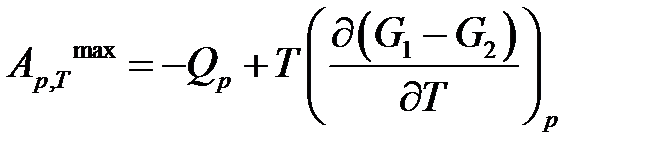
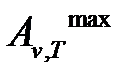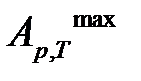Уравнения для и называются уравнениями максимальной работы Гиббса-Гельмгольца, в кото­рых часто индекс «mах» не пишут, т.к. знак равен­ства уже означает термодинамическую обратимость и, следо­вательно, – максимальную работу реакции.

В экспериментах было обнаружено, что чем ниже температура, тем меньше разность ( ).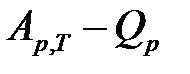

Однако равенство 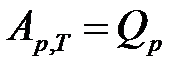соблюдается не только при температуре, равной нулю, но и вблизи нуля температур по шкале Кельвина, т.е.

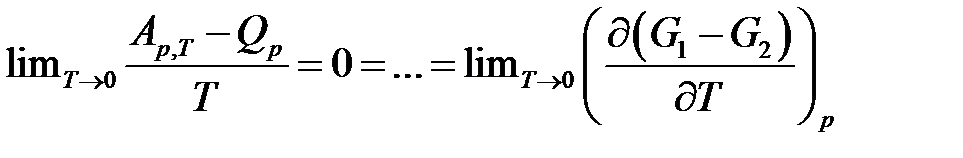
Этот постулат получил название тепловой теоремы Нернста.

По правилу Лопиталя (предел отношения функций равен пределу отношения их производных):

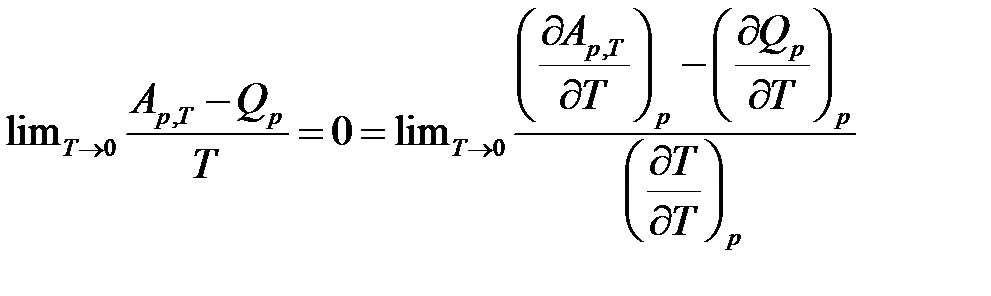
Раскрытие неопределённости типа 0/0 даёт:

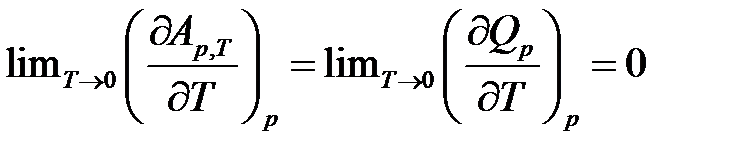
Ранее было установлено

A_p,T = (G₁–G₂)_p,T

Записав дополнительно

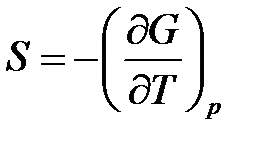
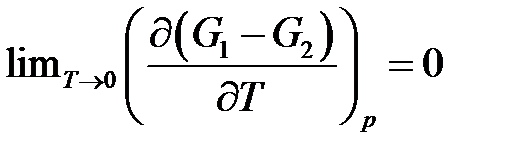
следует, что изменение энтропии вблизи нуля температурной шкалы Кельвина также равно нулю, т.е. 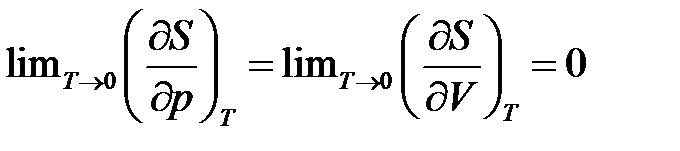(постулат Планка или третий закон термодинамики), т.е. энтропия перестаёт быть функцией состояния.

Фактически Планк предположил, что при температуре Т = 0 К не только алгебраическая сумма энтропии твердых тел, но и энтропия каждого тела в отдельности также равняется нулю .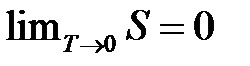

Формулировка третьего закона термодинамики по Планку:

в любом изотермическом процессе, который происходит при температуре, близкой к абсолютному нулю, изме­нение энтропии системы равно нулю.
Из положения теоремы Нернста о том, что энтропия системы вблизи Т = 0 К не изменяется, следу­ет, что в этой области не происходит теплообмена системы с окружающей средой (изотермический процесс является так­же и адиабатным).

Таким образом, система, еще не достигнув температуры Т = 0 К, приходит в такое состояние, что дости­жение абсолютного нуля практически становится не­возможным (как путем адиабатного расширения, так и путем изотермического процесса).

Нернст сделал вывод, являющийся формулировкой третьего закона термодинамики:

ни­каким конечным процессом нельзя охладить тело до абсолютного нуля,

или аб­солютный нуль температур недостижим.

Рассмотрим цикл Карно с температурой теплоотдатчика Т₁ = Т и температурой теплоприемника Т₂ = 0.

По второму закону термодинамики, для кругового процесса §dQ/T = 0 или

Δs₁₂ + Δs₂₃ + Δs₃₄ + Δs₄₁ = 0,

где Δs₁₂ = Q/T, Δs₂₃ = 0 (адиабатный процесс); Δs₃₄ = 0 (по постулату Планка), Δs₄₁ = 0 (ади­абатный процесс).

Следовательно, в результате прове­дения такого цикла, который дает воз­можность получать непрерывную рабо­ту за счет охлаждения одного теплоот­датчика, можно создать вечный двига­тель второго рода, что, согласно второму закону термодинамики, не­возможно.

Или: невозможно соз­дать машину, которая в качестве низшего источника теплоты имела бы тело с Т = 0 К,

или

вечный двигатель третьего рода неосуществим.

Поскольку 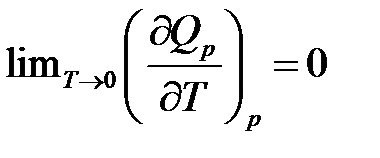, то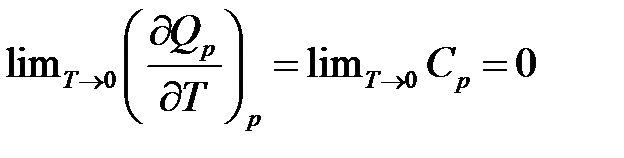

т.е. теплоемкость не изменяется вблизи абсолютного нуля и стремится к нулю.

А т.к. теплоёмкость равна нулю, то и изменения внутренней энергии вблизи абсолютного нуля не происходит, а соответственно аналитическому выражению первого закона термодинамики, и работа не совершается.