Стационарная теплопроводность в телах простейшей формы

Плоская стенка

При установившемся или стационарном тепловом режиме температура тела во времени остается постоянной, т.е. 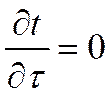. Если внутренние источники теплоты отсутствуют ( 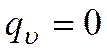), то уравнение Фурье имеет вид:

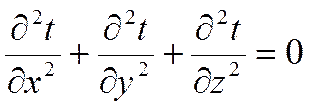
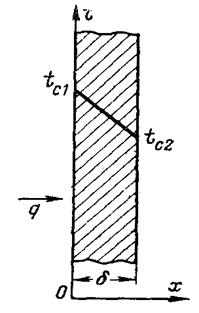Рассмотрим изотропную стенку толщиной δ, высота и ширина которой являются величинами бесконечно большими относительно толщины δ, с посто­янным коэффициентом теплопроводности λ. На наружных поверхностях стенки поддерживаются постоянными температуры t_с1 и t_с2.

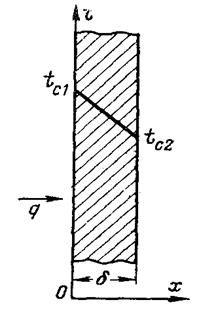При заданных условиях температура будет изме­няться только в направлении, перпендикулярном пло­скости стенки. Если ось Ох направить, как показано на рисунке, то температура в направлении осей Оуи Oz будет оставаться постоянной

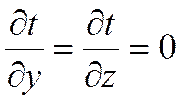
Температура будет функцией только одной координаты х и уравнение теплопроводности для рассматриваемого случая запишется

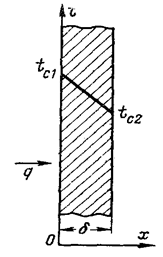
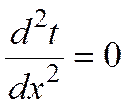
Зададим граничные условия в рассматриваемой задаче

при х = 0 t = t_с1

при х = δ t = t_с2

В результате решения поставленной задачи должно быть найдено распределение температуры в плоской стенке, т.е. t = f(x), и получена формула для определения количества теплоты, проходящего в единицу времени через стенку.

Закон распределения температур по толщине стенки найдется в ре­зультате двойного интегрирования уравнения Фурье.

Первое интегрирование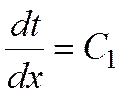

Второе интегрирование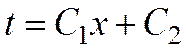

Постоянные С₁ и С₂ определяются из граничных условий:

при х = 0 и t = t_с1 С₂ = t_c1

при х = δ и t = t_с2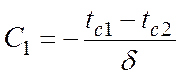

В итоге, закон распределения температуры в рассматриваемой плоской стенке

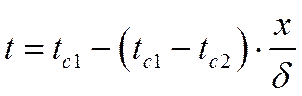
Для определения количества теплоты, про­ходящего через единицу поверхности стенки в единицу времени в направлении оси Ох, вос­пользуемся законом Фурье

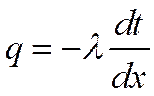, а

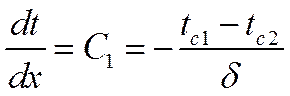
Следовательно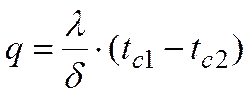

Из уравнения следует, что количество теплоты, проходящее через единицу поверхности стенки в единицу времени, прямо пропорцио­нально коэффициенту теплопроводности λ, разности температур на на­ружных поверхностях стенки (t_с1 – t_с2) и обратно пропорционально тол­щине стенки δ.

Отношение δ/λ, (м²·К)/Вт называется тепловым или термическим со­противлением стенки.

Зная плотность теплового потока, легко вычислить общее количество теплоты 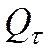, Дж, которое передаётся через поверхность стенки величиной F за промежуток времени τ

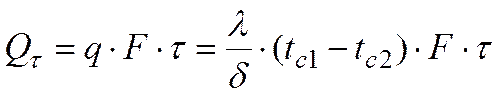
Рассмотрим теплопроводность многослойной плоской стенки, состо­ящей из n однородных слоев. Примем, что контакт между слоями со­вершенный и температура на соприкасающихся поверхностях двух сло­ев одинакова.

При стационарном режиме тепловой поток, проходящий через лю­бую изотермическую поверхность неоднородной стенки, один и тот же.

При заданных температурах на внешних поверхностях такой стенки, размерах слоев и соответствующих коэффициентах теплопроводно­сти можно составить систему уравнений

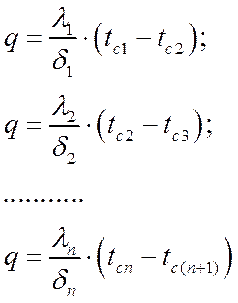
Выразив температурные напоры в каждом слое и сложив правые и левые части полученных уравнений, будем иметь

.

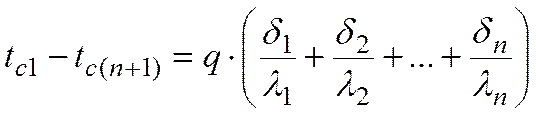Отсюда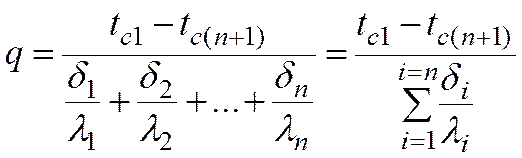

Величина 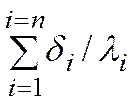, равна сумме термических сопротивлений всех n слоев, называется полным термическим сопротивлением теплопроводности многослойной стенки.

Цилиндрическая стенка

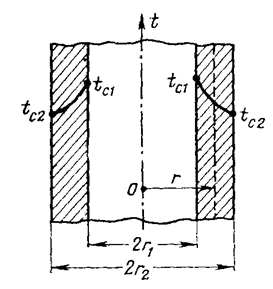Рассмотрим стационарный процесс теплопроводности в цилиндри­ческой стенке (трубе) с внутренним диаметром d₁=2r₁ и наружным ди­аметром d₂=2r₂.

На поверхностях стенки заданы постоянные температуры t_с1 и t_с2. В заданном интервале температур коэффициент теплопроводности ма­териала стенки λ является постоянной величиной.

Необходимо найти распределение температур в цилиндрической стенке и тепловой поток через нее.

В рассматриваемом случае дифференциальное уравнение теплопро­водности удобно записать в цилиндрической системе координат

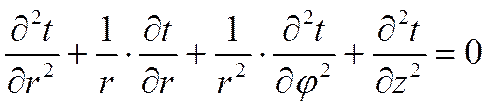
При этом ось Oz совмещена с осью трубы.

При заданных условиях температура изменяется только в радиаль­ном направлении и температурное поле будет одномерным. Поэтому

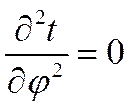и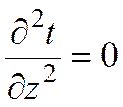

Уравнение Фурье примет вид

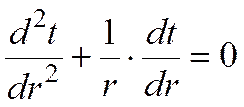
Граничные условия

при r = r₁ t = t_c1

при r = r₂ t = t_c2

Введём новую переменную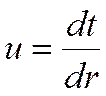

тогда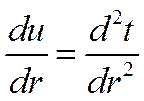

Подставляя в уравнение Фурье, получим

,

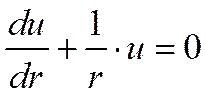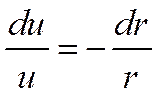
Интегрируя, получаем

^{-> -> ->} .

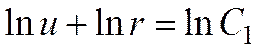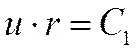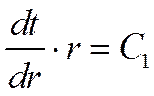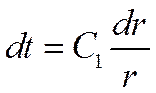После интегрирования

(*)

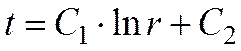Подставляя граничные условия

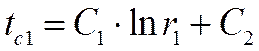
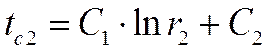
Решение уравнений дает

.

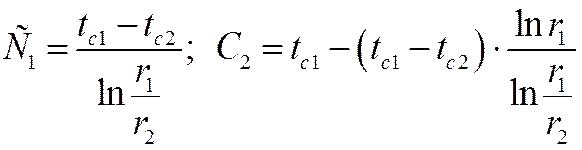Подставив значения С₁ и С₂ в уравнение (*), получим

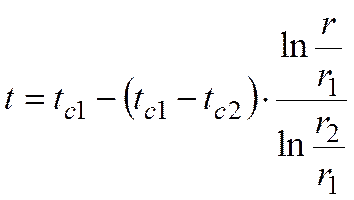или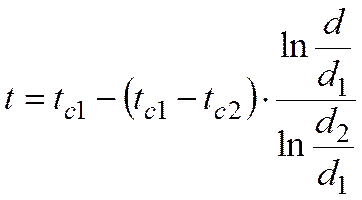

Для нахождения количества теплоты, Вт, прохо­дящего через цилиндрическую поверхность вели­чиной F в единицу времени, можно воспользо­ваться законом Фурье

.

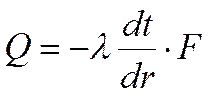Учитывая, что F=2π·r·l и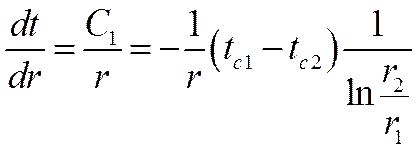

получаем 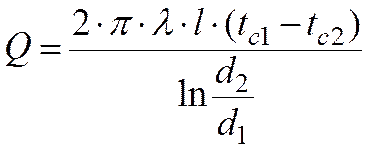, Вт.

Следовательно, количество теплоты, проходящее через цилиндрическую стенку в единицу времени, определя­ется заданными граничными условиями и не зависит от радиуса.

Тепловой поток Q может быть отнесен либо к единице длины трубы, либо к единице внутренней или внешней поверхности. При этом расчетные формулы для плотности теплового потока, Вт/м², прини­мают вид

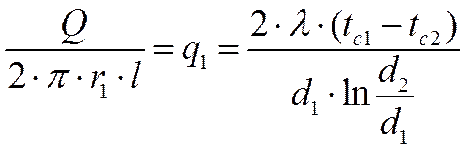
(тепловой поток через единицу внутренней поверхности);

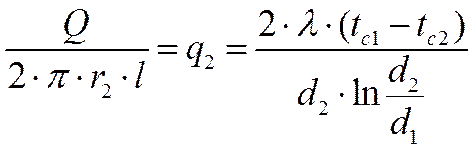
(тепловой поток через единицу наружной поверхности);

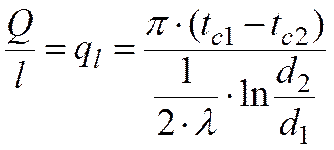
(тепловой поток, проходящий через единицу длины трубы, Вт/м).