Предикат. Операции над предикатами.
Неформально предикат можно определить как некоторое высказывание, значение которого зависит от значений предметных переменных из множества M, на котором определен предикат.
Примеры:
a) P(x) : “x есть простое число”;
(Здесь и всюду в дальнейшем для задания предиката будем использовать краткую форму записи, которая подробно расписывается следующим образом: 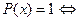 “x есть простое число”.)
“x есть простое число”.)
b) D(x,y) : “x нацело делится на y”;
c) R(x,y) : “x > y”.
В качестве предметного множества для этих примеров можно рассматривать любые числовые множества, в частности, в примерах a), b) – M = Í, а в c) – M = Ñ.
Более строго предикат можно определить как отображение n-ной степени множества M, называемой местностью или арностью предиката в двухэлементное множество B = {1, 0}
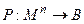 .
.
При подстановке в предикат 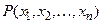 вместо предметных переменных набора значений
вместо предметных переменных набора значений 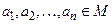 получим логическое высказывание (так
получим логическое высказывание (так 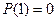 , а
, а 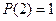 ). Таким образом, предикат представляет собой переменное высказывание (или систему высказываний), истинность которого определяется подстановкой различных значений предметных переменных.
). Таким образом, предикат представляет собой переменное высказывание (или систему высказываний), истинность которого определяется подстановкой различных значений предметных переменных.
Так как предикаты принимают значения из множества B, то для них определены логические операции 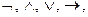 ~. Кроме того, для предикатов вводятся операции утверждения всеобщности и утверждения существования.
~. Кроме того, для предикатов вводятся операции утверждения всеобщности и утверждения существования.
Операция утверждение всеобщности ставит в соответствие высказывательной форме P(x) высказывание 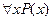 (читается как, P(x) истинно для всех x из множества M, на котором определен предикат). Высказывание
(читается как, P(x) истинно для всех x из множества M, на котором определен предикат). Высказывание 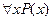 истинно тогда и только тогда, когда высказывание P(a) истинно для любого элемента
истинно тогда и только тогда, когда высказывание P(a) истинно для любого элемента 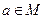 .
.
Операция утверждение существования ставит в соответствие высказывательной форме P(x) высказывание 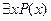 (читается как, существует такой x из множества M, для которого высказывание P(x) истинно). Высказывание
(читается как, существует такой x из множества M, для которого высказывание P(x) истинно). Высказывание 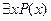 истинно тогда и только тогда, когда высказывание P(a) истинно хотя бы для одного элемента
истинно тогда и только тогда, когда высказывание P(a) истинно хотя бы для одного элемента 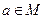 .
.
Знаки " и $ называются кванторами всеобщности и существование (квантор в переводе с латинского – определение количества). Переход от высказывательной формы P(x) к высказываниям 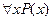 или
или 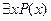 называется навешиванием квантора или связыванием переменной x (иногда – квантификацией переменной x). Переменная, на которую навешен квантор, называется связанной, несвязанная переменная называется свободной. Смысл связанных и свободных переменных в предикатных выражениях различен. Свободная переменная – это обычная переменная, которая может принимать различные значения из M, а выражение P(x) – переменное высказывание, зависящее от значения x. Выражения
называется навешиванием квантора или связыванием переменной x (иногда – квантификацией переменной x). Переменная, на которую навешен квантор, называется связанной, несвязанная переменная называется свободной. Смысл связанных и свободных переменных в предикатных выражениях различен. Свободная переменная – это обычная переменная, которая может принимать различные значения из M, а выражение P(x) – переменное высказывание, зависящее от значения x. Выражения 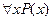 и
и 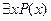 не зависят от переменной x и при фиксированных P и M имеют вполне определенное значение. Переменные, являющиеся по существу связанными, встречаются не только в математической логике. Например, в выражениях
не зависят от переменной x и при фиксированных P и M имеют вполне определенное значение. Переменные, являющиеся по существу связанными, встречаются не только в математической логике. Например, в выражениях 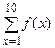 или
или 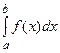 переменная x связана, при фиксированной f первое выражение равно определенному числу, а второе является функцией от a и b.
переменная x связана, при фиксированной f первое выражение равно определенному числу, а второе является функцией от a и b.
Таким образом, в высказываниях 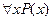 и
и 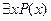 говорится не о свойствах отдельных элементов множества M, а о свойствах самого множества M. Истинность или ложность этих высказываний не зависит от того, как обозначена предметная переменная, входящая в них, и ее можно заменить любой другой предметной переменной, например y, и получить высказывания
говорится не о свойствах отдельных элементов множества M, а о свойствах самого множества M. Истинность или ложность этих высказываний не зависит от того, как обозначена предметная переменная, входящая в них, и ее можно заменить любой другой предметной переменной, например y, и получить высказывания 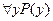 и
и 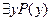 , имеющие тот же самый смысл и те же самые значения истинности, что и исходные высказывания.
, имеющие тот же самый смысл и те же самые значения истинности, что и исходные высказывания.
В общем случае для n-арного предиката, если 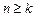 , операции утверждения всеобщности или существования можно выполнять k раз (порядок выбора переменных, по которым происходит навешивание квантора, может быть любым, исключая их повторение) и получить выражение
, операции утверждения всеобщности или существования можно выполнять k раз (порядок выбора переменных, по которым происходит навешивание квантора, может быть любым, исключая их повторение) и получить выражение
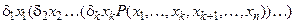 , (1)
, (1)
где 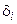 обозначает квантор всеобщности или существования. Переменные
обозначает квантор всеобщности или существования. Переменные 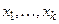 в высказывательной форме (1) являются связанными, а
в высказывательной форме (1) являются связанными, а 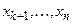 – свободными.
– свободными.
Высказывательная форма (1) при замене переменных 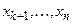 элементами множества M обращается в истинное или ложное высказывание. При k = n высказывательная форма (1) становится высказыванием. Изменение порядка следования различных кванторов изменяет смысл высказывания, что может изменить его истинностное значение.
элементами множества M обращается в истинное или ложное высказывание. При k = n высказывательная форма (1) становится высказыванием. Изменение порядка следования различных кванторов изменяет смысл высказывания, что может изменить его истинностное значение.
Например, для предиката делимости D(x,y):
высказывание 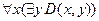 читается, как “для любого x существует y, такое, что x делится на y”, и является истинным высказыванием, так как любое натуральное x делится на себя и на 1, т.е. y = x или y =1;
читается, как “для любого x существует y, такое, что x делится на y”, и является истинным высказыванием, так как любое натуральное x делится на себя и на 1, т.е. y = x или y =1;
высказывание 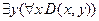 читается, как “существует y, на который делится любой x ”, и также является истинным высказыванием, так как на значение y =1 делится любое натуральное x.
читается, как “существует y, на который делится любой x ”, и также является истинным высказыванием, так как на значение y =1 делится любое натуральное x.
Дата добавления: 2016-02-09; просмотров: 1329;
