Нахождение обратной матрицы с помощью элементарных преобразований.

Справа к данной невырожденной матрице 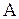приписать единичную матрицу 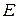того же порядка, что и матрица : .

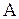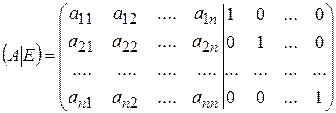Далее с помощью элементарных преобразований над строками объединенной матрицы 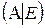привести матрицу 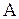к единичной матрице. Тогда на месте матрицы 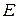окажется обратная матрица 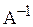, то есть будет получена матрица вида: .

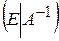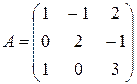Пример 2. Для матрицы из предыдущего примера найти обратную матрицу с помощью элементарных преобразований.

Решение. Так как 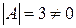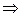обратная матрица существует.

Составим объединенную матрицу : .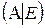

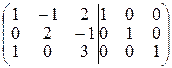Получим под главной диагональю нули: умножим все элементы первой строки на “-1” и прибавим их к соответствующим элементам третьей строки ( ):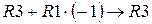

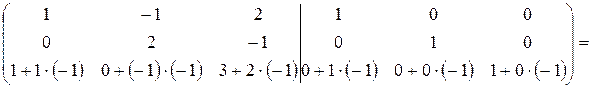
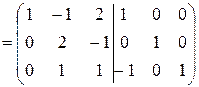
Поменяем местами вторую и третью строки: .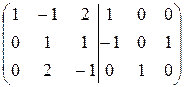

Умножим вторую строку на “-2” и прибавим ее к третьей строке ( ):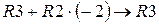

.

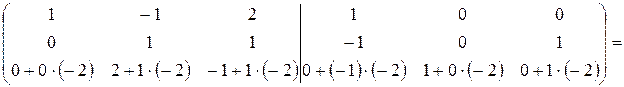
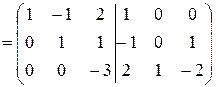Разделим третью строку на “-3” ( ): .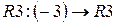

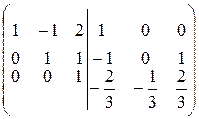Под главной диагональю получили нули на главной диагонали единицы.

Теперь получим нули над главной диагональю: умножим третью строку на “-1” и прибавим ее ко второй строке ( 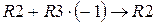); умножим третью строку на “-2” и прибавим ее к первой строке ( ):

.

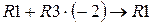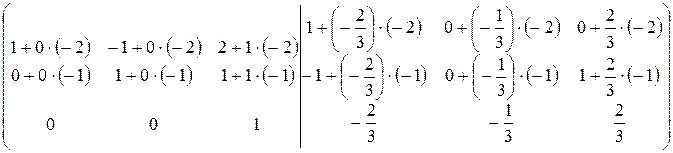
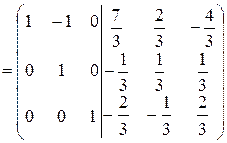Прибавим вторую строку к первой строке ( ):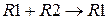

= .

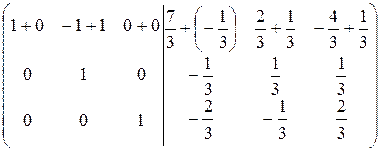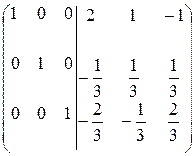Таким образом, получена матрица: .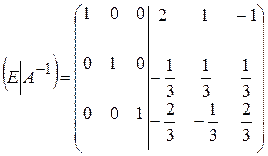

Следовательно, обратная матрица: .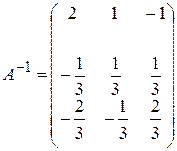

Полученную матрицу можно сравнить с матрицей из предыдущего примера рассчитанную другим способом (они совпадают).

Ранг матрицы

Пусть дана прямоугольная матрица 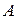размера 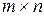: 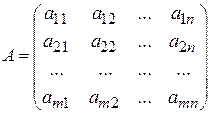. Выделим в этой матрице 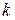произвольных столбцов, где ( 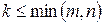“ка меньше либо равно меньшему из чисел 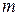или ”).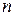

Определитель 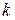- го (“катого”) порядка, составленный из элементов матрицы 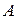, расположенных на пересечении выделенных строк и столбцов, называется минором 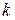- го порядка матрицы .

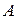Элементы матрицы 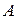являются минорами 1-го порядка.

Рассмотрим всевозможные миноры матрицы 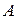, отличные от нуля.

Рангом матрицы 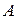называется наивысший порядок миноров данной матрицы, отличных от нуля.

Обозначение: 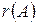или .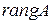

Свойства ранга матрицы:

1) если матрица 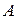имеет размеры 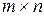, то ;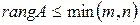

2) если все элементы матрицы 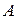равны нулю, то только в этом случае ;

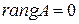3) если 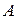– квадратная матрица 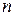– го порядка, то 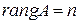только если .

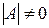Базиснымназывается минор, порядок которого определяет ранг матрицы.

У матрицы может быть несколько базисных миноров.

Если в матрице 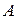имеется минор 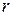– го (“эртого”) порядка, отличный от нуля, а все ее миноры 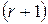– го (“эрплюспервого”) порядка, окаймляющие этот минор (то есть содержащие минор 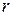– го порядка целиком внутри себя), равны нулю, то ранг матрицы 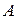равен 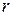и данный минор 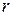– го порядка является базисным.