Нахождение обратной матрицы с помощью присоединенной.
Обратная матрица может быть найдена по формуле 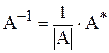 , где
, где 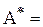
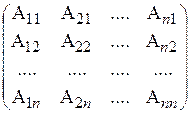 матрица, составленная из алгебраических дополнений элементов матрицы
матрица, составленная из алгебраических дополнений элементов матрицы 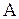 и транспонированная. Матрица
и транспонированная. Матрица 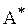 называется присоединенной для матрицы
называется присоединенной для матрицы 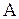 .
.
Пример 1. Найти матрицу обратную матрице 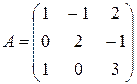 .
.
Решение. Сначала проверяем, является ли матрица невырожденной: 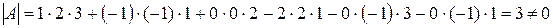
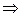 матрица невырожденная и для нее существует обратная.
матрица невырожденная и для нее существует обратная.
Найдем алгебраические дополнения для всех элементов матрицы 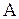 :
:
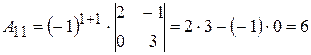 ;
; 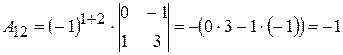 ;
;
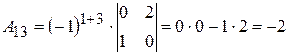 ;
; 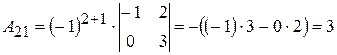 ;
;
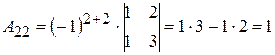 ;
; 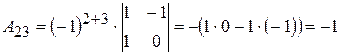 ;
;
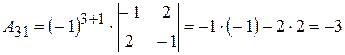 ;
; 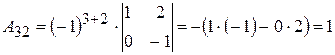 ;
; 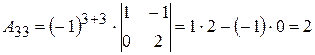 .
.
Составим матрицу 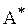 , учитывая, что она транспонированная:
, учитывая, что она транспонированная: 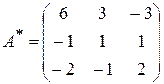 .
.
Получим обратную матрицу:
 .
.
Проверка: 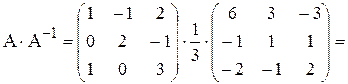
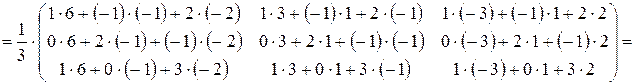
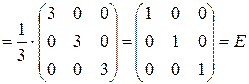 .
.
Элементарными преобразованиямистрок (столбцов) матрицы являются следующие:
1) отбрасывание нулевой строки (столбца);
2) умножение всех элементов строки (столбца) матрицы на число, отличное от нуля;
3) перестановка строк (столбцов) матрицы;
4) прибавление к одной строке (столбцу) другой строки (столбца), умноженной на любое число.
Две матрицы 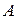 и
и 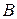 называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. Записывается
называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. Записывается 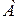 ~
~ 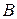 .
.
Дата добавления: 2016-02-09; просмотров: 952;
