Цифровые компараторы (устройства сравнения)
Цифровые компараторы относятся к арифметическим устройствам. Эти устройства выполняют сравнение двух чисел, заданных в двоичном (двоично-десятичном) коде. В зависимости от схемного исполнения компараторы могут определять только равенство двух многоразрядных чисел A и B или работать по более сложному алгоритму и выделять сигналы А = В, А > В, А < В.
Примером современного четырехразрядного компаратора служит микросхема K561ИП2. Схема имеет вид четырехразрядных входа А и В и при управляющих входа, задающих режим сравнения (равно, больше, меньше) — рис.5.41. При необходимости сравнения многоразрядных кодов компараторы каскадируются. Простейшее последовательное каскадирование показано на рис.5.41, б. При этом способе каскадирования задержки микросхем суммируются и если критерий быстродействия является определяющим, переходят к более сложной схеме параллельного (пирамидального) каскадирования.
Сумматоры
Сумматоры являются основой арифметических устройств и представляют собой комбинационную схему, осуществляющую суммирование двоичных кодов. Многоразрядные суммирующие схемы строятся на основе одноразрядных сумматоров.
Простейшим суммирующим элементом является полусумматор. Он имеет два входа A и B для двух слагаемых и два выхода: суммы S и переноса Р. Таблица истинности сумматора следующая:
| Входы | Выходы | ||
| А | В | S | P |
Выражение логической функции для суммы S представляет собой значение операции «Исключающее ИЛИ», иначе называемой сложением по модулю 2:
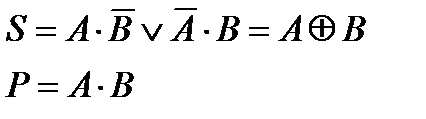
Функциональная схема полусумматора показана на рис.5.42. Полусумматор функционирует без учета сигнала переноса с предыдущих младших разрядов. Схема, осуществляющая учет сигнала переноса, называется полным сумматором. Сумматор работает в соответствии со следующей таблицей истинности:
| Входы | Выходы | |||
| Аi | Bi | Pi–1 | Si | Pi |
 Логические функции, описывающие получение сигнала суммы и переноса в произвольном разряде двоичного кода:
Логические функции, описывающие получение сигнала суммы и переноса в произвольном разряде двоичного кода:
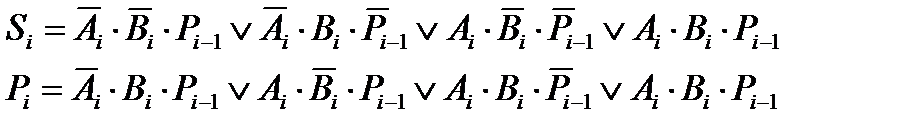
Последние уравнения поддаются минимизации, в результате которой получается:
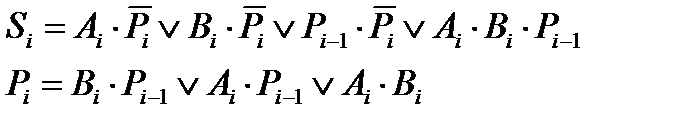
Функциональная схема, решающая полученные уравнения, приведена на рис.5.43. Эта схема является базовым узлом многоразрядных сумматоров.
На рис.5.44 показан серийный 4-разрядный сумматор К561ИМ1, осуществляющий одновременное (параллельное) суммирование 4 двоичных разрядов. Для увеличения разрядности суммируемых слов такие сумматоры каскадируются последовательным включением сигналов переноса, но такое каскадирование связано с задержкой распространения сигнала переноса по всей цепочке микросхем. Время переноса можно уменьшить, используя специальные блоки ускоренного (сквозного) переноса, что реализуется при конструировании ЭВМ.
Вычитатели двоичных кодов в виде самостоятельных изделий не производятся. На практике операция вычитания заменяется сложением уменьшаемого с вычитаемым, представленными в дополнительном коде.
Контроль четности
Существуют специальные цифровые микросхемы для проверки паритета двоичных чисел, суть которой состоит в суммировании по модулю два всех разрядов числа с целью выяснения четности или нечетности. Эта операция позволяет повысить надежность передачи двоичной информации.
Информация передается всегда четным (при четном паритете) или нечетным (при нечетном паритете) числом, для этого дополнительно к информационным разрядам слова добавляют специальный паритетный разряд. Содержание паритетного разряда таково, чтобы довести число единиц слова до четного (или нечетного). На приемной стороне принятый код проверяется на сохранение паритета. Считается, что искажение сигнала может проявиться только в одном разряде. Паритетная проверка не обнаруживает ошибок, возникающих в двух разрядах одновременно, но вероятность таких ошибок мала. В ответственных случаях могут использоваться специальные методы кодирования сигналов. Устройства для проверки четности двоичных слов выпускаются в виде самостоятельных элементов в нескольких сериях микросхем. На рис. 5.45 показана микросхема 564СА1, определяющая паритет двоичного слова длиной до 12 разрядов. Она имеет 12 информационных D0 – D11 и один управляющий V входы и один выход S. Все входы логически равнозначны и порядок подключения разрядов слова не играет роли. Сигнал на управляющем входе V задает режим работы схемы по паритету: при V = 0 обеспечивается четный паритет, т.е. S = 0 при четном числе единиц и S = 1 при нечетном. При V = 1 имеет место нечетный паритет, обратный рассмотренному. Если в слове менее 12 разрядов, на свободных входах должно быть четное число единиц при проверке на четность и нечетное — при проверке на нечетность.
Микросхемы позволяют проводить каскадирование, соединяя выход S предыдущей схемы с входом V последующей.
Дата добавления: 2016-02-09; просмотров: 1886;
