Основы алгебры логики
Все цифровые электронные преобразователи построены на базе логических элементов, соединенных между собой в определенные функциональные схемы. Цифровые логические элементы характеризуются конечным числом значений своего выходного параметра, чаще всего двумя значениями. Переменная X, которая может принимать то или иное значение из набора двух значений (0, 1) называется логической. Функция f (х1, х2,... хn) логических переменных может принимать тоже только одно значение из набора (0, 1) и называется логической функцией (двоичной, переключательной).
В основе синтеза и анализа логических схем лежит специальный математический аппарат — алгебра Буля или алгебра логики. Аппарат алгебры логики широко используется в теории цифровых вычислительных схем. При этом физическая природа сигнала значения не имеет, важно лишь то, что сигнал может иметь одно из двух возможных значений. Например, сигнал с высоким уровнем напряжения принимается за логическую единицу, а с низким уровнем — за логический нуль. Причем, цифры 0 и 1 характеризуют состояние логического элемента и не содержат никакой количественной оценки его свойств, поэтому их не следует рассматривать как числа в обычном арифметическом смысле.
В алгебре логики используют логические функции одной и двух переменных, с помощью которых путем суперпозиции можно построить любую логическую функцию.
Для одной переменной x существует 4 логические функции:
1. Константа нуль. 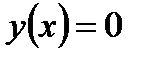 независимо от состояния переменной х.
независимо от состояния переменной х.
2. Константа единица. 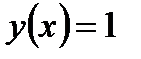 независимо от состояния переменной х.
независимо от состояния переменной х.
3. Инверсия (отрицание). 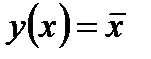 Это значит, что
Это значит, что 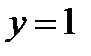 при
при 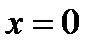 и
и 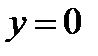 при
при 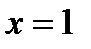 .
.
4. Функция повторениям 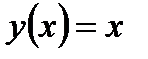 .
.
Для двух переменных существует 16 логических функции 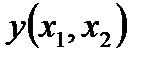 :
:
1. Константа нуль. 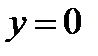 независимо от состояния переменных x1 и x2;.
независимо от состояния переменных x1 и x2;.
2. Константа единица. 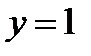 независимо от состояния переменных x1 и x2.
независимо от состояния переменных x1 и x2.
3. Переменная 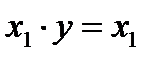 независимо от состояния переменной x2.
независимо от состояния переменной x2.
4. Переменная 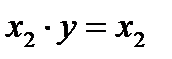 независимо от состояния x1.
независимо от состояния x1.
5. Конъюнкция (логическое умножение, И). 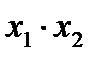 или
или 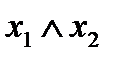
Функция y приобретает единичное значение только в том случае, если обе переменных имеют единичное значение. В остальных случаях она равна нулю.
| x1 | ||||
| x2 | ||||
| y |
6. Дизъюнкция (логическое сложение, ИЛИ). 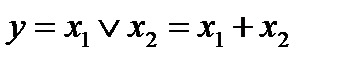 .
.
Функция принимает единичное значение, если любая переменная имеет единичное значение
| x1 | ||||
| x2 | ||||
| y |
7. Инверсия x1 (отрицание x1, НЕ x1). 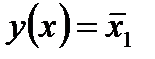 . Функция у принимает единичное значение, если переменная x1, имеет нулевое значение независимо от состояния переменной x2.
. Функция у принимает единичное значение, если переменная x1, имеет нулевое значение независимо от состояния переменной x2.
| x1 | ||||
| x2 | ||||
| y |
8. Инверсия x2 (НЕ x2). 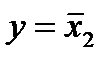
| x1 | ||||
| x2 | ||||
| y |
9. Операция Пирса, 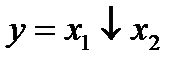 . Функция у приобретает единичное значение только в случае, если ни x1 ни x2 не имеет единичного значения, т.е.
. Функция у приобретает единичное значение только в случае, если ни x1 ни x2 не имеет единичного значения, т.е. 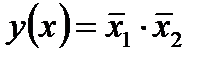
| x1 | ||||
| x2 | ||||
| y |
10. Операция Шеффера. 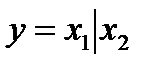 . Функция у приобретает нулевое значение, если x1 и x2 одновременно имеют единичное значение. В остальных случаях она имеет единичное значение, т.е.
. Функция у приобретает нулевое значение, если x1 и x2 одновременно имеют единичное значение. В остальных случаях она имеет единичное значение, т.е. 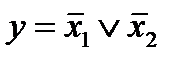 .
.
| x1 | ||||
| x2 | ||||
| y |
11. Сумма по mod 2 (неравнозначность). 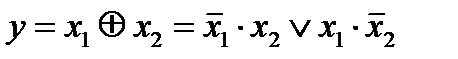
| x1 | ||||
| x2 | ||||
| y |
12. Логическая равнозначность. 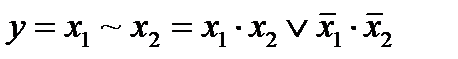
| x1 | ||||
| x2 | ||||
| y |
13. Операция запрета по 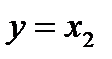
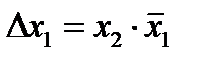 .
.
| x1 | ||||
| x2 | ||||
| y |
14. Операция запрета по 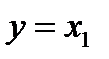
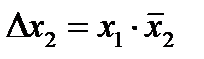
| x1 | ||||
| x2 | ||||
| y |
15. Импликация от x1 к x2. 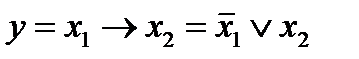
| x1 | ||||
| x2 | ||||
| y |
16. Импликация от x2 к x1. 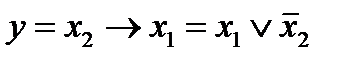
| x1 | ||||
| x2 | ||||
| y |
Для алгебры логики, как и для обычной алгебры, действительны следующие законы:
1. Переместительный (коммутативности):
Для логического сложения 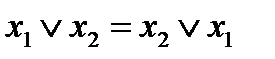
Для логического умножения 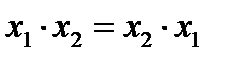 .
.
2. Сочетательный (ассоитивный):
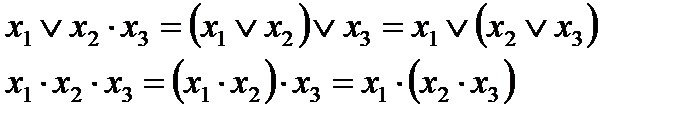
3. Распределительный (дистрибутивности):
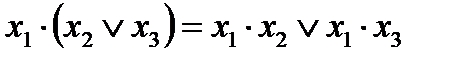
4. Инверсии (де-Моргана):
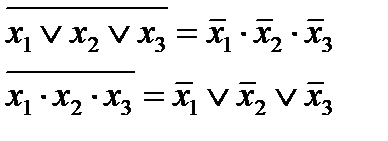
В синтезе логических цепей понятие инверсии и инверсного преобразования играют значительную роль. Очень часто оказывается значительно проще реализовать инверсную структуру, чем требуемую. С помощью законов алгебры логики осуществляется анализ и синтез логических цепей.
Дата добавления: 2016-02-09; просмотров: 849;
