Основные положения теории подобия.

МЕТОДЫ ФИЗИЧЕСКОГО МОДЕЛИРОВАНИЯ.

Общие положения.

Моделирование как метод исследования широко используют в различных областях современного естествознания и техники: аэромеханике, гидравлике, теплотехнике, самолето- и ракетостроении, различных областях машиностроения, гидротехническом строительстве и т. д.

Модели - это инженерные представления, которые могут быть материализованы в виде физических моделей или сформулированы математически.

Исходя из этого по принципам, на которых основано моделирование, различают моделирование двух видов: физическое и математическое.

Физическое моделирование предусматривает воссоздание в физической модели тех же самых или аналогичных физических полей, что действуют и в объекте натуры, лишь измененных по своим абсолютным значениям в соответствии с масштабом моделирования. Одним из основных преимуществ физического моделирования является возможность осуществления прямых наблюдений за моделируемыми процессами и явлениями, иногда это преимущество является решающим.

В физическом моделировании выделяетсяаналоговое моделирование, котороепредусматривает замену в модели по сравнению с натурой одних физических полей другими, например замену натурного поля механических напряжений электрическим полем в модели или замену поля механических напряжений картиной оптической анизотропии в оптически чувствительных прозрачных материалах. Таким образом, на аналоговых моделях изучают закономерности явлений и процессов, протекающих в натурных объектах, используя математическую аналогию различных по физической природе процессов, т. е. математическую тождественность основных законов, совпадение дифференциальных уравнений, описывающих эти процессы.

В отличие от физического моделированияматематическое моделирование предусматривает построение некоторых идеализированных схем или, другими словами, математических моделей исследуемых процессов или явлений и их исследование аналитическими методами. Исходя из этого, методы математического моделирования относят к теоретическим методам исследования. Такая точка зрения доминирует в геомеханике.

Вообще моделирование получило в геомеханике широкое развитие вследствие ряда объективных обстоятельств.

Как уже указывалось, массив горных пород является весьма сложной средой, которая к тому же находится под одновременным воздействием большого числа факторов как естественного, так и техногенного происхождения.

В результате в различных частях одного и того же участка породного массива при ведении горных работ одновременно могут происходить процессы деформирования самого различного характера - процессы упругого деформирования, необратимые пластические деформации и, наконец, процессы смещений и разрушений пород с разрывом сплошности. Кроме того, в каждой конкретной точке выработки или массива имеет место своя конкретная ситуация, своё сочетание действующих факторов и поэтому результаты натурных исследований, как правило, всегда имеют некоторый, иногда весьма существенный разброс, и вследствие этого могут обладать недостаточной общностью.

К этому следует добавить, что в натурных условиях обычно весьма ограничены возможности варьирования параметрами системы, технологией и последовательностью ведения горных работ, тогда как при моделировании можно проследить влияние основных параметров в самых широких пределах.

Вместе с тем при построении любого вида моделей воспроизводятся только общие, принципиально существенные особенности изучаемых явлений и чётко отбираются действующие факторы, которыми в процессе модельных исследований можно варьировать. Применительно к такому объекту, как горные породы, например, невозможно воспроизвести микротрещиноватость и мелкоблоковую трещиноватость, даже при очень крупных масштабах моделирования.

Таким образом, учитывая преимущества и недостатки обоих подходов, можно сказать, что оптимальное сочетание натурных исследований с моделированием позволяет всесторонне исследовать изучаемые процессы и явления, выявить как общие закономерности, так и влияние отдельных факторов и при этом существенно сэкономить материальных затраты и время.

Физическое моделирование бывает двух родов: с увеличением и с уменьшениеммасштаба системы. В геомеханике, изучающей, как правило, объекты весьма больших размеров, применяют моделирование второго рода, т. е. с уменьшением абсолютных размеров объектов.

При решении задач геомеханики методами моделирования обычно испытывают серию моделей, причем используя наиболее эффективный для решения поставленной задачи метод, испытывают модели разных масштабов. Например, сначала на моделях мелкого масштаба изучают общие закономерности процессов геомеханики в пределах всего участка массива, подверженного влиянию выработки, а затем на моделях крупного масштаба с большей детальностью изучают закономерности процессов в более локальной области массива, например, процессов взаимодействия пород кровли с крепью очистной выработки. При этом обычно в модели крупного масштаба воспроизводят лишь некоторую часть массива, а действие веса остальной части массива до поверхности компенсируют с помощью пригрузки, осуществляемой нагрузочными приспособлениями различного типа.

Основные положения теории подобия.

В основе методов моделирования лежит учение о подобии, основы которого заложены еще И Ньютоном.

Чтобы получить корректные результаты необходимо обеспечить подобие модели и натуры, т. е.

а) подобие геометрических свойств систем;

б) пропорциональность физических констант, имеющих существенное значение в изучаемом процессе;

в) подобие начального состояния систем;

г) подобие условий на границах систем в течение всего рассматриваемого периода процесса;

д) равенство определяющих критериев, при этом определяющими критериями подобия являются те, которые имеют существенное значение в изучаемом процессе.

При характеристике того или иного механического процесса механическое подобие может быть определено заданием переходных множителей или масштабов для длин (геометрическое подобие), для времени (кинематическое подобие) и для масс (динамическое подобие).

Для двух подобных систем условие геометрического подобия состоит в том, что все размеры пространства, занятого системой в модели, и размеры отдельных элементов модели изменены в определенное число m_L раз по сравнению с соответствующими размерами натуры:

L_м / L_н= m_L ,(10.1)

где L_миL_н - соответственно линейные размеры модели и натуры.

Условие кинематического подобия этих систем состоит в том, что любые сходственные точки (частицы) систем, двигаясь по геометрически подобным траекториям, проходят геометрически подобные пути в промежутки времени Т, отличающиеся постоянным множителемm_Т

Т_м / Т_н= m_Т. (10.2)

Условие динамического подобия систем состоит в том, что массы любых сходственных частиц этих систем отличаются друг от друга постоянным множителемm_М

М_м / М_н= m_М.(10.3)

Особенности объектов геомеханики состоят в том, что при заданном геометрическом масштабе моделирования (m_L = L_м / L_н) для обеспечения механического подобия модели и натуры необходимо отказаться в модели либо от равенства s_м = s_н, либо от равенства g_м = g_н, либо от равенства обоих показателей.

Если сохранить в модели равенство напряжений натуре (другими словами, равенство механических свойств материала модели и натуры), т.е. условие s_м = s_н, то необходимо обеспечить, чтобы объемный вес материала был больше в число раз, обратное геометрическому масштабу.

Например, при геометрическом масштабе модели m_L = L_м / L_н = 1/100 объемный вес материала модели должен быть равен

L_н1

g_м = --------- g_н = --------- g_н = 100g_н.(10.4)

L_мm_L

Условие (10.4) можно выполнить, применив в модели натуральные горные породы и придав им фиктивный объемный вес (100g_н в приведенном случае при m_L = 1/100) с помощью инерционных сил, которые могут быть созданы, например, путем вращения модели в центрифуге при соответствующем значении центробежной силы. Этот метод был предложен в 1932 г. профессорами Г. И. Покровским и Н. Н. Давиденковым и носит название метода центробежного моделирования.

Если же в модели применить некоторые искусственные материалы, механические характеристики которых ниже соответствующих характеристик моделируемых горных пород, т. е. отказаться от равенства s_м = s_н, то для обеспечения условий механического подобия модели и натуры необходимо

L_мg_м

s_м = ------- . -------s_н.(10.5)

L_нg_н

Искусственные материалы, соответствующие механические характеристики которых в принятом геометрическом масштабе моделирования удовлетворяют по отношению к моделируемым горным породам условию (10.5), называют материалами - эквивалентами данным горным породам или эквивалентными материалами. Метод же моделирования, основанный на применении эквивалентных материалов и предложенный в 1936 г. проф. Г. Н. Кузнецовым, носит название метода эквивалентных материалов.

При моделировании системы в соответствующем геометрическом масштабе продолжительность тех или иных процессов обычно изменяется. В связи с этим существенно важное значение имеет вопрос о масштабе времени при моделировании, который в общем случае определяется, исходя из приведенного выше условия кинематического подобия двух систем (10.2).

В тех случаях, когда на моделях воспроизводят сразу несколько процессов, масштабы времени для отдельных из них могут оказаться неодинаковыми В таких случаях масштаб времени устанавливают, исходя из соблюдения подобия в протекании лишь тех процессов, которые в решаемой задаче являются основными и не учитывают малозначащие элементы.

Нагружение физических моделей осуществляется:

* созданием усилий на контуре модели при помощи механических и гидравлических домкратов или заданием деформаций контура посредством жёстких ограничителей;

* собственным весом модели массива;

* посредством центробежных сил, возникающих в центрифуге;

* с помощью сил сопротивления сдвигу, как это делается в моделях с фрикционной базой.

Последний метод был предложен Р. Гудманом в 1971 г., такие модели представляют собой плоские установки, в которых гравитационные силы имитируются силами трения, возникающими при протягивании ленты под моделью объектов (рис.10.1).

 

 

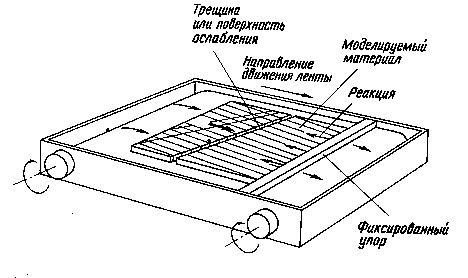
Рис. 10.1. Установка с фрикционной базой.

 

При этом сила веса моделируется силами трения, возникающими при протяжке ленты под моделью, упирающейся в фиксированную планку.