Полного тензора напряжений массива пород.
В наиболее общем виде, как было показано ранее, напряженное состояние в какой-либо точке массива может быть описано тензором напряжений Тs в виде матрицы его компонентов:
| sх | tху | tхz |
| tyx | sy | tyz |
| tzx | tzy | sz |
где sх, sy и sz - нормальные, а tху, tхz, tyx, tyz, tzx, tzy - касательные напряжения.
Матрица тензора напряжений может быть выражена главными нормальными напряжениями s1;s2; s3:
| s1 | ||
| s2 | ||
| s3 |
Для решения задач геомеханики, учитывая проявление в одних случаях только гравитационных, а в других - как гравитационных, так и тектонических сил, удобно присваивать индексы 1, 2 и 3 в матрице тензора таким образом, чтобы главное напряжение в вертикальном направлении обозначалось s3, наибольшее по модулю главное горизонтальное напряжение (в случае действия тектонических сил) - s1, другое главное горизонтальное напряжение - s2. Направления действия главных нормальных напряжений называют главными осями напряжений.
Таким образом, главное напряжение в вертикальной плоскости s3 всегда определяется весом пород вышележащей толщи и в случае различных плотностей (объемных весов) покрывающих пород имеет вид:
H
s3 = S gi hi(4.1)
0
где gi - объемный вес i-го слоя пород; hi - мощность i-го слоя; Н - глубина рассматриваемой точки от дневной поверхности.
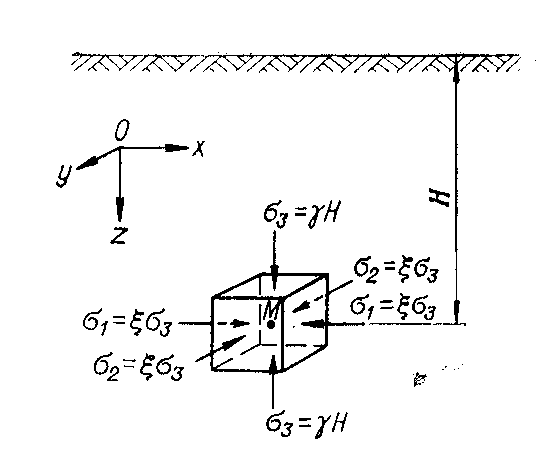
Если напряженное состояние массива пород определяется только действием гравитационных сил, то каждый элементарный объем (рис. 4.3) под действием
|
Рис. 4.3. Схема к расчету гравитационных напряжений в массиве пород.
вертикального гравитационного напряжения s3 будет испытывать деформации сжатия в вертикальном (по оси Оz) и деформации растяжения в горизонтальных направлениях (по осям Ох и Оу). Однако последним препятствует реакция окружающих пород, в результате чего возникают горизонтальные сжимающие напряжения s1 и s2, численно равные
n
s1 = s2 = x g H = --------- g H.(4.2)
1 - n
Здесь коэффициент x называется коэффициентом бокового давления или коэффициентом бокового отпора.. Этот коэффициент показывает, какую часть вертикальной нагрузки, действующей в рассматриваемой точке массива, составляют силы или напряжения, действующие в горизонтальной плоскости.
Для горных пород коэффициент поперечных деформаций nизменяется в пределах от 0.08 до 0.5, соответственно крайние возможные пределы изменения x составляют от 0,1 до 1. Следует подчеркнуть, что в соответствии с физическим смыслом коэффициента v, его значения не могут превышать 0.5, поэтому и значения коэффициента бокового давления x не могут быть больше 1. В противном случае среда теряет свою сплошность.
Это положение имеет принципиальное значение и должно использоваться при анализе и интерпретации результатов натурных измерений.
При слоистом строении массива значения горизонтальных напряжений s1 и s2 определяются конкретными значениями коэффициентов поперечных деформаций ni для соответствующего слоя. В связи с этим, если вертикальное напряжение s3 будет монотонно возрастать по мере увеличения глубины рассматриваемых слоев, то горизонтальные напряжения s1 и s2 при общей тенденции возрастания могут как увеличиваться, так и уменьшаться при переходе от слоя к слою.
Главное напряжение s3, обусловленное действием гравитационных сил, может в отдельных случаях отклоняться от вертикали вследствие наклонного залегания отдельных слоев пород, их складчатости и различной мощности, а также при сложном рельефе поверхности или наличии пустот в недрах. Отклонения эти обычно не превышают нескольких градусов, в редких случаях достигая 10 - 15°.
Изменение горизонтальной составляющей гравитационного поля напряжений по глубине характеризуется градиентом гравитационных напряжений Dsг, который также является функцией средней плотности пород, слагающих массив, и составляет 0,25 - 0,32 кгс / (см2.м).
Предельные значения n= 0,5 и x = l выражают, как это следует из формулы (4.2), условие гидростатического распределения напряжений в массиве, т. е. такого распределения, когда
s1 = s2 = s3(4.3)
Гидростатическое напряженное состояние является частным случаем напряженного состояния массива и характерно для таких пород, как глины, слабые глинистые и песчаные сланцы, каменные соли, слабые угли, способных к вязкопластическому течению при сравнительно невысоких нагрузках. По мнению многих исследователей, весьма прочные породы по мере роста глубины и связанного с ним роста давлений и температур также постепенно переходят в пластическое состояние, так что на достаточно больших глубинах распределение напряжений приближается к гидростатическому независимо от состава пород, слагающих массив. Однако в случае весьма прочных скальных пород эти глубины исчисляются, по-видимому, десятками километров, т. е. значительно больше глубин, реально достижимых при горных разработках.
Дата добавления: 2016-02-09; просмотров: 674;
