Основные характеристики корректирующих кодов

К основным характеристикам корректирующих кодов относят: избыточность кода, кодовое расстояние, число обнаруживаемых и исправляемых ошибок, корректирующие возможности кодов.

Принцип обнаружения и исправления ошибок кодами хорошо иллюстрируется с помощью геометрических моделей. Любой n – элементный двоичный код можно представить n–мерным кубом (рис.12.2), в котором каждая вершина отображает кодовую комбинацию, а длина ребра куба соответствует одной единице. В таком кубе расстояние между вершинами (кодовыми комбинациями) измеряется минимальным количеством ребер, находящимся между ними, обозначается d и называется кодовым расстоянием Хемминга.

Таким образом, кодовое расстояние – это минимальное число элементов, в которых любая кодовая комбинация отличается от другой (по всем парам кодовых слов). Например, код состоит из комбинаций 1011, 1101, 1000 и 1100. Сравнивая первые две комбинации, путем сложения их по модулю два находим, что d = 2. Сравнение первой и третьей комбинаций показывает, что и в этом случае d = 2. Наибольшее значение d = 3 обнаруживается при сравнении первой и четвертой комбинаций, а наименьшее d = 1 – второй и четвертой, третьей и четвертой комбинаций. Таким образом, для данного кода минимум расстояния d_min = 1.

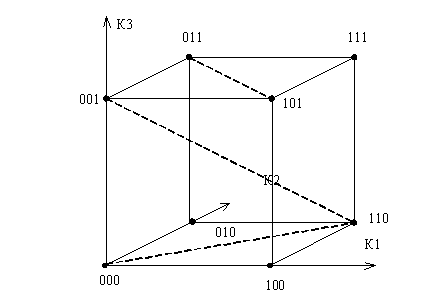
Рис. 12.2. Геометрическая модель двоичных кодов

В общем случае кодовое расстояние между двумя комбинациями двоичного кода равно числу единиц, полученных при сложении этих комбинаций по модулю два. Такое определение кодового расстояния удобно при большой разрядности кодов. Так, складывая комбинации

,

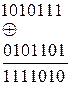определим, что кодовое расстояние между ними d = 5.

Если использовать все восемь кодовых комбинаций, записанных в вершинах куба, то образуется двоичный код на все сочетания. Такой код является непомехоустойчивым, так как любое искажение приводит к кодовой комбинации, принадлежащей данному сомножеству, а следовательно, искажение не будет обнаружено. Если же уменьшить число используемых комбинаций с восьми до четырех, то появится возможность обнаружения одиночных ошибок. Для этого выберем только такие комбинации, которые отстоят друг от друга на расстоянии d = 2, например, 000, 110, 011, 101. Остальные кодовые комбинации не используются. Если передавалась комбинация 101, а принята комбинация 100, то очевидно, что при приеме произошла ошибка. Таким образом, для обнаружения искажений необходимо все кодовые комбинации разделить на две группы: разрешенные и запрещенные.

Из приведенного примера можно сделать вывод, что способность кода обнаруживать и исправлять ошибки обусловлена наличием избыточности, которая обеспечивает минимальное расстояние между любыми двумя разрешенными комбинациями 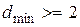, т.е. к исходной k – элементной комбинации необходимо добавить r контрольных символов, сформированных по определенным правилам.

Пусть на вход кодирующего устройства поступает последовательность из k информационных двоичных символов. На выходе ей соответствует последовательность из n = k + r двоичных символов.

Всего может быть 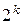разрешенных кодовых комбинаций и 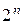различных выходных последовательностей, а следовательно, 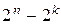возможных выходных последовательностей для передачи не используются и являются запрещенными комбинациями.

Искажение информации в процессе передачи сводится к тому, что некоторые из переданных символов заменяются другими. Так как каждая из 2^k разрешенных комбинаций в результате действия помех может трансформироваться в любую другую, то всего имеется 2^k×2ⁿ возможных случаев передачи (рис. 10.3). В это число входят: 2^k случаев безошибочной передачи (на рис. 10.3 обозначены жирными линиями):

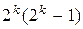случаев перехода в другие разрешенные комбинации, что соответствует необнаруженным ошибкам (на рис. 10.3 обозначены пунктирными линиями);

Рис. 12.3. Возможные варианты трансформаций кодовых комбинаций X_i в B_j

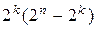случаев перехода в запрещенные комбинации, которые могут быть обнаружены (на рис. 12.3 обозначены штрихпунктирными линиями). Следовательно, число обнаруживаемых ошибочных кодовых комбинаций от общего числа возможных случаев передачи составляет:

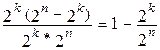. (12.1)

Отношение числа исправляемых кодом ошибочных кодовых комбинаций к числу обнаруживаемых ошибочных комбинаций равно:

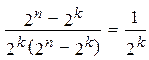. (12.2)

Из приведенных выше рассуждений можно сделать вывод, что коррекция ошибок возможна благодаря введению избыточности, которая определяется выражением:

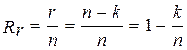. (12.3)

Эта величина показывает, какую часть от общего числа символов кодовой комбинации составляют контрольные символы. В теории кодирования величину k/n принято называть скоростью передачи [5]. Необходимо отметить, что величина k/n характеризует относительную скорость передачи информации. Если производительность источника информации равна 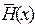бит/с, то скорость передачи после кодирования этой информации окажется равной

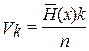. (12.4)

Для обнаружения или исправления значительного числа ошибок, необходимо иметь код с большим числом проверочных символов. При этом существенно возрастает длительность кодовых блоков, что приводит к задержке информации при передаче и приеме.

Если длительность помехи превосходит длительность элементарного сигнала, то искажается несколько символов, и такой вид искажений называется пакетом (пачкой) искажений. Под пакетом искажений длиной b понимается такой вид комбинации помехи, в которой между крайними разрядами, пораженными помехами, содержатся b – 2 разряда. Например, при b = 4 пакет искажений может иметь вид: 1001 (поражены только два крайних символа), 1111 (поражены все символы), 1011 (не поражен лишь один символ). При любом варианте непременным условием пакета данной длины является поражение крайних символов.

Кодовое расстояние, как отмечалось выше, является основной характеристикой корректирующей способности данного кода. Если код используется только для обнаружения ошибок кратности m, то необходимо и достаточно, чтобы минимальное расстояние удовлетворяло условию

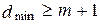. (12.5)

Под кратностью ошибки понимают число позиций кодовой комбинации, в которых под действием помехи одни символы оказались замененными другими.

Для исправления ошибки кратностью S необходимо, чтобы минимальное расстояние удовлетворяло условию

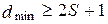. (10.6.)

Корректирующие коды можно одновременно использовать и для обнаружения и для исправления ошибок. В этом случае кодовое расстояние должно удовлетворять условию

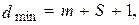(10.7)

где всегда должно выполняться условие m > S.

Вопрос о минимально необходимой избыточности, при которой код обладает нужными корректирующими свойствами, является одним из важнейших в теории кодирования. Для некоторых частных случаев Хемминг указал простые соотношения, позволяющие определить необходимое число проверочных символов:

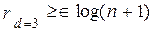, (12.8)

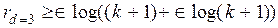, (12.9)

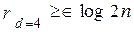, (12.10)

где знак 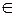означает округление в большую сторону.