Сравнение известных способов скрытой передачи информации
Проведём сравнительный анализ работоспособности способов скрытой передачи информации с помощью хаотической синхронизации, рассмотренных в настоящем обзоре. Для проверки эффективности этих методов при наличии шума используем численное моделирование и оценим некоторые количественные характеристики работоспособности схем.
Основными количественными характеристиками работоспособности схем скрытой передачи информации являются:
а) Критическое значение 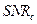 отношения энергии на бит к спектральной плотности мощности шума (SNR), при котором схема передачи данных становится неработоспособной, т.е. оказывается невозможным восстановление исходного полезного цифрового сигнала m(t) по получаемому на выходе сигналу
отношения энергии на бит к спектральной плотности мощности шума (SNR), при котором схема передачи данных становится неработоспособной, т.е. оказывается невозможным восстановление исходного полезного цифрового сигнала m(t) по получаемому на выходе сигналу 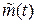 . Отношение энергии на бит к спектральной плотности шума, которое вводится в рассмотрение для цифровых систем связи, является аналогом отношения сигнал/шум в аналоговой связи:
. Отношение энергии на бит к спектральной плотности шума, которое вводится в рассмотрение для цифровых систем связи, является аналогом отношения сигнал/шум в аналоговой связи:
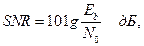 (11.10)
(11.10)
где 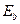 – энергия сигнала, приходящаяся на один бит передаваемой информации,
– энергия сигнала, приходящаяся на один бит передаваемой информации, 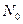 – спектральная плотность мощности шума. При этом энергия, приходящаяся на один бит, описывается как:
– спектральная плотность мощности шума. При этом энергия, приходящаяся на один бит, описывается как:
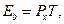 (11.11)
(11.11)
где 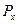 – мощность передаваемого сигнала в отсутствие шума,
– мощность передаваемого сигнала в отсутствие шума, 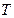 – время передачи одного бита, а спектральная мощность шума определяется как:
– время передачи одного бита, а спектральная мощность шума определяется как:
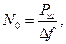 (11.12)
(11.12)
где 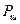 – мощность шума в канале связи,
– мощность шума в канале связи, 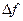 – ширина полосы пропускания канала. Так как шумы неизбежно присутствуют в каналах связи реальных устройств, оценка работоспособности схем передачи информации при наличии шумов является очень важной и актуальной задачей.
– ширина полосы пропускания канала. Так как шумы неизбежно присутствуют в каналах связи реальных устройств, оценка работоспособности схем передачи информации при наличии шумов является очень важной и актуальной задачей.
б) для характеристики степени устойчивости схем скрытой передачи информации по отношению к внешним шумам в цифровых системах связи достаточно часто используют, наряду с характеристикой, описанной выше, зависимость вероятности ошибки на бит (BER – Bit Error Rate) от отношения энергии на бит к спектральной плотности мощности шума. Вероятность ошибки на бит характеризует качество передачи информации и представляет собой количество ошибок, отнесённое к числу переданных битов. Предположим, что схема корректно передаёт бинарный бит 0 с вероятностью 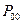 и бинарный бит 1 с вероятностью
и бинарный бит 1 с вероятностью 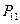 . Тогда ошибочное диагностирование бинарного бита 1 при передаче бинарного бита 0 характеризуется вероятностью
. Тогда ошибочное диагностирование бинарного бита 1 при передаче бинарного бита 0 характеризуется вероятностью 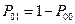 , а вероятность
, а вероятность 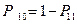 характеризует ошибочное диагностирование бинарного бита 0 при передаче бинарного бита 1. Если символы появляются в передаваемой последовательности с вероятностями
характеризует ошибочное диагностирование бинарного бита 0 при передаче бинарного бита 1. Если символы появляются в передаваемой последовательности с вероятностями 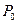 и
и 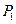 соответственно, то вероятность ошибки на бит вычисляется следующим образом:
соответственно, то вероятность ошибки на бит вычисляется следующим образом:
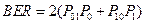 (11.13)
(11.13)
причем вероятности 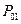 и
и 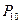 зависят от типа и параметров системы связи.
зависят от типа и параметров системы связи.
в) максимальное значение РМС расстройки управляющих параметров (РМ, %) генераторов, которые изначально должны быть идентичными. Как уже обсуждалось в разделах 11.7.1 и 11.7.2, в большинстве случаев такие генераторы должны располагаться на различных сторонах канала связи. Ввиду сложности технической реализации таких устройств влияние расстройки их управляющих параметров на эффективность работы способов передачи информации является весьма актуальной проблемой.
г) максимальный уровень нелинейных искажений в канале связи, при котором схема работает:
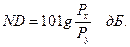 (11.14)
(11.14)
Здесь 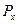 – мощность сигнала
– мощность сигнала 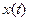 на выходе передающего генератора,
на выходе передающего генератора, 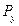 – мощность сигнала
– мощность сигнала 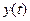 на входе принимающего устройства. Традиционно в численных расчётах используются нелинейные искажения в виде кубической нелинейности
на входе принимающего устройства. Традиционно в численных расчётах используются нелинейные искажения в виде кубической нелинейности 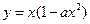 .
.
Для того чтобы количественно сравнить способы скрытой передачи информации, описанные в настоящем разделе, оценим вышеупомянутые характеристики для всех рассмотренных схем.
Результаты расчёта количественных характеристик работоспособности схем представлены в таблице 11.1.
Как видно из таблицы, схема 11.19, описанная в разделе 11.7.4, становится неработоспособной при отношении энергии на бит к спектральной плотности шума 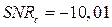 дБ, в то время как для других рассмотренных нами схем
дБ, в то время как для других рассмотренных нами схем 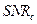 оказывается положительным. То есть при наличии в канале связи шумов определённого уровня (даже если мощность шумов меньше мощности передаваемого сигнала) большинство схем становится неработоспособным. Понятно, что значения таких характеристик будут меняться от схемы к схеме. Из схем 11.13–11.17 лучшими в этом отношении являются схемы на основе переключения хаотических режимов и модулирования управляющих параметров (схемы 11.14 и 11.16,
оказывается положительным. То есть при наличии в канале связи шумов определённого уровня (даже если мощность шумов меньше мощности передаваемого сигнала) большинство схем становится неработоспособным. Понятно, что значения таких характеристик будут меняться от схемы к схеме. Из схем 11.13–11.17 лучшими в этом отношении являются схемы на основе переключения хаотических режимов и модулирования управляющих параметров (схемы 11.14 и 11.16, 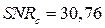 дБ). Но положительное значение отношения энергии на бит к спектральной плотности шума свидетельствует об ограниченной устойчивости к шумам и деструктивной роли шума при передаче информации.
дБ). Но положительное значение отношения энергии на бит к спектральной плотности шума свидетельствует об ограниченной устойчивости к шумам и деструктивной роли шума при передаче информации.
Схема 11.19, описанная в разделе 11.7.4, обладает значительной устойчивостью к шумам в канале связи. При этом, ещё более искажая передаваемый сигнал, шум препятствует третьей стороне декодировать информационное сообщение. В этом случае можно говорить о конструктивной роли шума в повышении конфиденциальности передачи информации, тогда как в остальных случаях роль шума является деструктивной.
Таблица 11.1 – Критические значения отношения энергии на бит к спектральной плотности шума 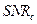 , расстройки управляющих параметров
, расстройки управляющих параметров 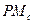 изначально идентичных генераторов и уровня нелинейных искажений в канале связи
изначально идентичных генераторов и уровня нелинейных искажений в канале связи 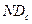
| № рисунка | Название схемы | 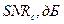
| 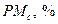
| 
|  Раздел* Раздел*
| Литература |
| 11.13 | Хаотическая маскировка | 56,48 | 0,30 | 1,03 | 11.7.1.1 | [25] |
| 11.14 | Переключение хаотических режимов | 30,76 | 2,00 | 23,3 | 11.7.1.2 | [145] |
| 11.15 | Нелинейное подмешивание | 64,99 | 0,30 | 0,26 | 11.7.1.3 | [146] |
| 11.16 | Модулирование управляющих параметров | 30,76 | 2,00 | 23,3 | 11.7.1.4 | [147] |
| 11.18 | Схема на основе режима фазовой синхронизации | 32,40 | 0,80 | 10,7 | 11.7.3 | [155] |
| 11.17 | Схема на основе режима обобщённой синхронизации | 39,52 | 1,00 | 7,75 | 11.7.2 | [109] |
| 11.19 | Сверхустойчивая к шумам схема | –10,01 | 2,00 | 27,2 | 11.7.4 | [162] |
Справедливость вышеприведённых рассуждений подтверждается также зависимостью вероятности ошибки на бит от спектральной плотности мощности шума для различных схем скрытой передачи информации. Указанные зависимости представлены на рисунке 11.20.
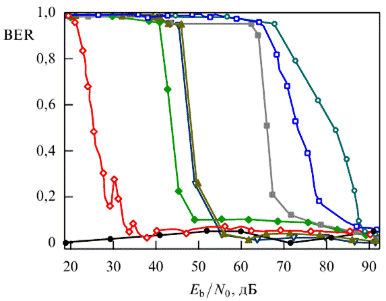
Рисунок 11.20 – Зависимости вероятности ошибки на бит (BER) от отношения энергии на бит к спектральной плотности мощности шума ( 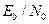 )) для различных схем скрытой передачи информации: ○– хаотическая маскировка, ♦ – переключение хаотических режимов (модулирование управляющих параметров), ■ – нелинейное подмешивание, ◊ – схема на основе режима фазовой синхронизации (кривая частично перенесена из работы [155], ▲ – схема на основе режима обобщённой синхронизации.
)) для различных схем скрытой передачи информации: ○– хаотическая маскировка, ♦ – переключение хаотических режимов (модулирование управляющих параметров), ■ – нелинейное подмешивание, ◊ – схема на основе режима фазовой синхронизации (кривая частично перенесена из работы [155], ▲ – схема на основе режима обобщённой синхронизации.
При расчёте вероятности ошибки на бит пороговое значение, позволяющее восстановить исходную последовательность бинарных битов
по сигналу 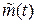 , выбиралось фиксированным независимо от интенсивности шума, воздействующего на систему, тогда как при определении характеристик, представленных в таблице, оно менялось. В то же время, как видно из
, выбиралось фиксированным независимо от интенсивности шума, воздействующего на систему, тогда как при определении характеристик, представленных в таблице, оно менялось. В то же время, как видно из
рисунка 11.20, для различных способов скрытой передачи информации (схемы 11.13–11.18 таблицы) вероятность ошибки на бит достаточно быстро становится равной 1, тогда как для сверхустойчивого к шуму способа (схема 11.19) она оказывается близкой к 0, вне зависимости от интенсивности шума, воздействующего на систему, что достаточно хорошо согласуется с результатами, представленными выше.
Оценим теперь влияние расстройки управляющих параметров на эффективность работы рассмотренных способов скрытой передачи данных.
Подобные оценки позволяют заключить, что схема на основе режима обобщённой синхронизации (см. раздел 11.7.4) будет оставаться работоспособной до тех пор, пока генераторы принимающего устройства не будут расстроены более чем до 2 % по параметру 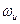 . Конечно, это не столь большая величина, и в этом отношении рассматриваемая схема имеет конкурентов, которыми снова являются схемы передачи информации на основе переключения хаотических режимов и модулирования управляющих параметров (схемы 11.14 и 11.16 в таблице соответственно). Однако схема 11.19 и с этой точки зрения обладает принципиальным преимуществом перед схемами 11.14 и 11.16. Изначально идентичные хаотические генераторы в схемах 2 и 4 таблицы (так же как и во всех остальных, кроме схемы 9) должны располагаться на различных сторонах канала связи (для возможности реализации режима полной синхронизации между ними). В схеме 11.19 идентичные генераторы располагаются только на принимающей стороне канала связи, что позволяет легко осуществить при необходимости их юстировку.
. Конечно, это не столь большая величина, и в этом отношении рассматриваемая схема имеет конкурентов, которыми снова являются схемы передачи информации на основе переключения хаотических режимов и модулирования управляющих параметров (схемы 11.14 и 11.16 в таблице соответственно). Однако схема 11.19 и с этой точки зрения обладает принципиальным преимуществом перед схемами 11.14 и 11.16. Изначально идентичные хаотические генераторы в схемах 2 и 4 таблицы (так же как и во всех остальных, кроме схемы 9) должны располагаться на различных сторонах канала связи (для возможности реализации режима полной синхронизации между ними). В схеме 11.19 идентичные генераторы располагаются только на принимающей стороне канала связи, что позволяет легко осуществить при необходимости их юстировку.
Что касается устойчивости к нелинейным искажениям в канале связи, то и по этой характеристике рассмотренная в разделе 11.7.4 схема превосходит все известные аналоги. Понятно, что чем больше влияние нелинейных искажений на сигнал, тем выше должен быть максимально допустимый уровень нелинейных искажений, при котором способ скрытой передачи данных будет оставаться ещё работоспособным. Как видно из таблицы, максимальный уровень нелинейных искажений для схемы 11.19 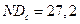 дБ. Наиболее близкими показателями опять обладают способы скрытой передачи информации на основе переключения хаотических режимов и модулирования управляющих параметров (схемы 11.14 и 11.16), однако устойчивость схемы 11.19 к нелинейным искажениям оказывается несколько выше. Кроме того, схемы 11.14 и 11.16 обладают ограниченной устойчивостью к шумам, в то время как устойчивость схемы 11.19 является практически неограниченной в реальных пределах.
дБ. Наиболее близкими показателями опять обладают способы скрытой передачи информации на основе переключения хаотических режимов и модулирования управляющих параметров (схемы 11.14 и 11.16), однако устойчивость схемы 11.19 к нелинейным искажениям оказывается несколько выше. Кроме того, схемы 11.14 и 11.16 обладают ограниченной устойчивостью к шумам, в то время как устойчивость схемы 11.19 является практически неограниченной в реальных пределах.
11.7.6. Экспериментальная реализация схем передачи информации
с помощью хаотической синхронизации
Следует отметить, что большинство публикаций в этой области свидетельствуют о том, что работы по применению хаотической синхронизации носит теоретический и лабораторно–экспериментальный характер. Наиболее продвинутыми являются работы по скрытой передаче информации на большие расстояния с помощью хаотической синхронизации на основе существующих коммерческих волоконно–оптических каналов связи.
Остановимся на описании этого эксперимента более подробно, так как данную работу следует признать одной из наиболее интересных на сегодня экспериментальных реализаций идей передачи информации на основе полной хаотической синхронизации в оптическом диапазоне.
В качестве источников хаотических сигналов с большой размерностью аттрактора и высокой информационной энтропией использовались генераторы на основе полупроводниковых диодов с запаздывающей обратной связью, которая реализовывалась двумя различными способами, а именно, рассматривались электронно– оптическая и полностью оптическая обратные связи. Использование двух типов обратной связи в генераторе хаоса оптического диапазона позволило реализовать два способа передачи информации, описанных выше: нелинейное подмешивание информационного сигнала к хаотическому и модулирование параметров хаотического сигнала информационным сигналом. В первом случае (схема соответствующего эксперимента приведена на рисунке 11.21) излучение лазерного диода ЬО проходит через интегрированный электро–оптический интерферометр Маха–Зендера MZI, который управляется электро–оптической запаздывающей обратной связью (включающей в себя линию задержки DL, фотодиод PD и электронный усилитель A) и работает как нелинейный модулятор лазерного излучения. Информационный сигнал в этом случае подмешивается к сигналу обратной связи через волоконно–оптический смеситель OFС. Выходной хаотический сигнал генератора, содержащий информационное сообщение, дополнительно усиливается перед подачей в канал связи для достижения необходимого уровня мощности. Во втором случае (рисунок 11.22) источником лазерного излучения снова является лазерный диод LD, а оптическая обратная связь реализуется с помощью зеркала R, коэффициент отражения которого нелинейно зависит от интенсивности падающего излучения. Длина внешнего резонатора системы составляла 6 м.
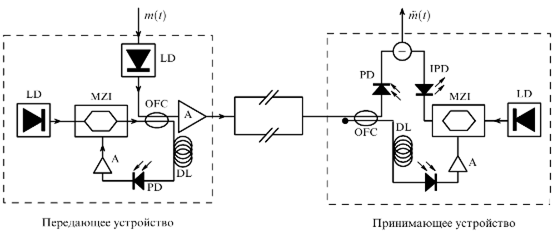
Рисунок 11.21 – Экспериментальная схема скрытой передачи информации в оптическом диапазоне на основе нелинейного подмешивания сигнала к хаотическому
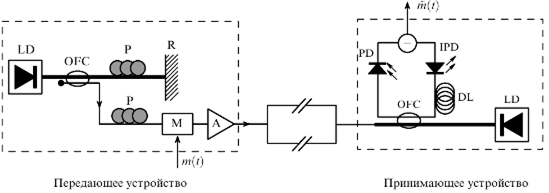
Рисунок 11.22 – Экспериментальная схема скрытой передачи информации в оптическом диапазоне на основе модулирования параметров передающего генератора информационным сигналом
В резонатор помещался поляризатор Р для обеспечения необходимой поляризации света, отражённого от зеркала R с переменным коэффициентом отражения. Информационный сигнал вводился посредством модуляции параметров хаотического сигнала с помощью модулятора М. Затем передаваемый по оптическому каналу сигнал усиливался, как и в первой схеме. В схемах также имелись не показанные на рисунках фильтры для подавления влияния шумов, связанных со спонтанной эмиссией.
В обеих схемах полезный информационный сигнал декодировался в принимающем устройстве путём достижения режима полной хаотической синхронизации между генераторами на различных сторонах канала связи. Основной проблемой эксперимента стало создание близких к идентичным генераторов на обоих концах канала связи. В обеих схемах наибольшие сложности при достижении идентичности генераторов вызывали активные элементы генераторных схем, а именно полупроводниковые лазеры. В экспериментах использовались лазеры с длинами волн 1552,0 и 1552,9 нм в приёмном и передающем устройствах соответственно. Для обеспечения одинаковых длин волн и стабильной работы лазерных диодов для каждого из лазеров подбирался свой температурный режим, который поддерживался в течение всего эксперимента. Подбор с высокой степенью идентичных пассивных элементов не вызывал принципиальных сложностей. При достаточно точной настройке параметров оптических генераторов хаоса в однонаправленно связанной системе наблюдалось устойчивое возникновение режимов полной хаотической синхронизации при достаточной мощности сигнала, подаваемого на принимающее устройство [232]. Было показано, что расстройка генераторов на различных сторонах канала связи для устойчивости работы схемы передачи информации (для достижения полной хаотической синхронизации) не может превышать 3 %. При передаче сигнала на большие расстояния возникала проблема разрушения режима синхронизации из–за влияния дисперсии в волоконно–оптическом канале связи (она составляла в рассматриваемом эксперименте порядка –850 пс нм–1). В связи с этим на выходе канала используемой коммерческой волоконно-оптической сети перед подачей сигнала на приёмное устройство вводились отрезки волоконно- оптических линий с дисперсией другого знака, компенсирующие дисперсионное искажение сигнала, а также дополнительные усилители для обеспечения необходимого уровня мощности (данные элементы не показаны на рисунках 11.21 и 11.22).
Вероятность ошибки на бит (BER) для данной экспериментальной схемы с нелинейным подмешиванием информационного сигнала к хаотическому составляет 10–7 при скорости передачи информации 3 Гб с–1. Аналогичные результаты получены и при использовании схемы с модулированием параметров, однако при той же величине BER = 10–7 скорость передачи оказалась почти в три раза меньше (  1 Гб с–1).
1 Гб с–1).
Полученные результаты представляются весьма важными и открывают серьёзные перспективы применения схем передачи информации с использованием хаотической синхронизации в оптическом диапазоне в современных информационно–телекоммуникационных системах. Все исследования были выполнены на основе уже существующих телекоммуникационных сетей, т.е. внедрение соответствующих технологий не требует принципиальной замены уже созданного оборудования, что чрезвычайно важно для практического использования. К недостаткам рассматриваемой схемы следует отнести сравнительно низкую скорость передачи данных, что, как обсуждалось выше, связано с общими недостатками подобных схем скрытой передачи информации, а именно с необходимостью достижения режимов полной хаотической синхронизации, которые весьма чувствительны к расстройке хаотических генераторов на различных сторонах телекоммуникационного канала и шумам, всегда присутствующим в реальных экспериментах.
В заключение раздела 11.7 следует сказать, что генераторы хаоса могут быть построены на основе систем Росслера, Чуя, Лоренца, кольцевых схем, клистронов, и лазеров.
12. КОДИРОВАНИЕ ИНФОРМАЦИИ ПРИ ПЕРЕДАЧЕ
ПО ДИСКРЕТНОМУ КАНАЛУ С ПОМЕХАМИ
Постановка задачи
Действие помехи на дискретный сигнал с конечным числом элементов приводит к количественным и качественным изменениям его структуры (к ошибкам в числе и состоянии элементов). Чтобы обеспечить в таких условиях передачу информации с заданной достоверностью, возможные ошибки должны быть обнаружены, а если требуется, то и исправлены.
Теория помехоустойчивого кодирования базируется на результатах исследований, проведенных Шенноном и сформулированных им в виде теоремы:
1. При любой производительности источника сообщений, меньшей, чем пропускная способность канала, существует такой способ кодирования, который позволяет обеспечить передачу всей информации, создаваемой источником сообщений, со сколь угодно малой вероятностью ошибки.
2. Не существует способа кодирования, позволяющего вести передачу информации со сколь угодно малой вероятностью ошибки, если производительность источника сообщений больше пропускной способности канала.
С доказательством теоремы можно ознакомиться в [4]. Теорема устанавливает теоретический предел возможной эффективности системы при достоверной передаче информации. Ею опровергнуто казавшееся интуитивно правильным представление о том, что достижение сколь угодно малой вероятности ошибки в случае передачи информации по каналу с помехами возможно лишь при введении бесконечно большой избыточности, то есть при уменьшении скорости передачи до нуля. Из теоремы следует, что помехи в канале не накладывают ограничений на точность передачи. Ограничение накладывается только на скорость передачи, при которой может быть достигнута сколь угодна высокая достоверность передачи.
Теорема неконструктивна в том смысле, что в ней не затрагивается вопрос о путях построения кодов, обеспечивающих указанную идеальную передачу.
Следует отметить, что при любой конечной скорости передачи информации вплоть до пропускной способности сколь угодно малая вероятность ошибки достигается лишь при безграничном увеличении длительности кодируемых последовательностей знаков. Таким образом, безошибочная передача при наличии помех возможна лишь теоретически. На практике степень достоверности и эффективности ограничивается двумя факторами: размерами и стоимостью аппаратуры кодирования и временем задержки передаваемого сообщения. В настоящее время используются относительно простые методы кодирования, которые не реализуют возможностей, указанных теорией. Однако постоянно растущие требования к достоверности передачи и внедрение специализированных больших интегральных схем позволяют надеяться на то, что будут созданы эффективные устройства кодирования.
Таким образом, помехоустойчивое кодирование представляет собой обширную область теоретических и прикладных исследований. К числу основных задач, возникающих при этом, относятся отыскание кодов, эффективно исправляющих ошибки требуемого вида, нахождение методов кодирования и декодирования, способов их реализации.
Все коды разделяются на коды с обнаружением ошибок и коды с исправлением ошибок (корректирующие коды).
Задачи корректирующего кодирования обычно решают при следующих предположениях: избыточность эффективного кода равна нулю, кодирование выполняется двоичными сигналами, характеристики дискретного двоичного канала известны, канал является симметричным, то есть вероятности перехода нуля в единицу и единицы в нуль одинаковы.
Коды с обнаружением и исправлением ошибок подробно будут рассматриваться в курсе «Телемеханика». Здесь мы остановимся лишь на основных характеристиках корректирующих кодов и на базе одного из кодов покажем принцип обнаружения и исправления искажений.
Дата добавления: 2016-02-04; просмотров: 1905;
