Широкополосные усилители. Идеальное предельное и оптимальное согласование. Теория Фано
Наличие реактивных элементов в реальных сопротивлениях нагрузки (например, сопротивления антенны) приводит к возникновению теоретических ограничений на широкополосное согласование комплексных нагрузок.
Существует связь между шириной рабочей полосы частот и отдаваемой мощностью для каждого типа нагрузки.(теория Фано).

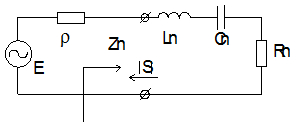 Пусть, например, к генератору Е с внутренним сопротивлением
Пусть, например, к генератору Е с внутренним сопротивлением 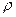 подключена комплексная нагрузка как на рисунке 1.18 Очевидно, что на частоте
подключена комплексная нагрузка как на рисунке 1.18 Очевидно, что на частоте 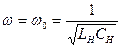 ,
,
при Rн= 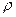 будет максимальная передача мощности в нагрузку. Случай, т.н. идеального согласования. Коэффициент отражения
будет максимальная передача мощности в нагрузку. Случай, т.н. идеального согласования. Коэффициент отражения 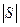 в этом случае равен нулю (рисунок 1.19,а).
в этом случае равен нулю (рисунок 1.19,а).

 |
При отклонении
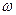 от
от 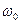 реактивное сопротивление контура Lн Сн растет,
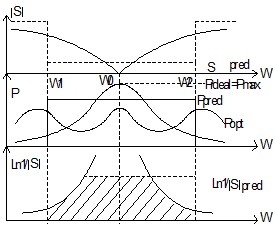
реактивное сопротивление контура Lн Сн растет, 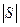 растет, активная мощность в нагрузке падает (рисунок 1.19,б). Сущность теоретических ограничений на согласование сводится к следующему. Если построить для этого случая функцию Ln
растет, активная мощность в нагрузке падает (рисунок 1.19,б). Сущность теоретических ограничений на согласование сводится к следующему. Если построить для этого случая функцию Ln 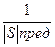 , то можно доказать, что площадь под этой кривой конечна и определяется элементами нагрузки. Если задан диапазон частот
, то можно доказать, что площадь под этой кривой конечна и определяется элементами нагрузки. Если задан диапазон частот 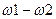 , то наиболее естественной предельной формой частотной характеристики является прямоугольная.
, то наиболее естественной предельной формой частотной характеристики является прямоугольная.
Формулы Фано, связывающие максимально допустимую полосу согласования 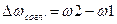 , с мерой рассогласования
, с мерой рассогласования 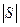 и параметрами генератора и нагрузки при прямоугольной частотной характеристике имеют вид
и параметрами генератора и нагрузки при прямоугольной частотной характеристике имеют вид
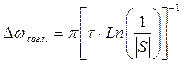 .
.
Из приведенного выражения следует, что
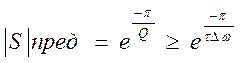 ,
,
где 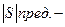 предельное значение коэффициента отражения в полосе частот
предельное значение коэффициента отражения в полосе частот 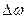 при заданных параметрах нагрузки, Q- добротность цепи нагрузки,
при заданных параметрах нагрузки, Q- добротность цепи нагрузки, 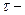 постоянная времени этой цепи,
постоянная времени этой цепи, 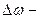 полоса согласования.
полоса согласования.
Для случая (рис.1.18) имеем
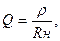
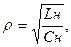
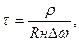
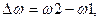
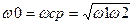
Если 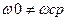 то следует к нагрузке подключить Lдоп. Или Cдоп.
то следует к нагрузке подключить Lдоп. Или Cдоп.
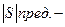 предельное значение модуля коэффициента отражения для других нагрузок определяется также, только меняется выражение для Q.
предельное значение модуля коэффициента отражения для других нагрузок определяется также, только меняется выражение для Q.
Таким образом, зная 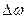 и параметры нагрузки можно сразу определить
и параметры нагрузки можно сразу определить 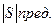 и предельную мощность
и предельную мощность 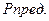 , которую можно передать в эту нагрузку в заданной полосе частот. Расчет
, которую можно передать в эту нагрузку в заданной полосе частот. Расчет 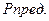 называют предельным согласованием
называют предельным согласованием
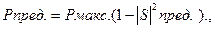
где 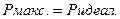 (см.рис.1.19,б)
(см.рис.1.19,б)
Такое согласование будет соответствовать построению согласующей цепи с 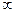 количеством элементов.
количеством элементов.
Синтез широкополосных согласующих цепей с частотными характеристиками мощности приближающихся к предельной прямоугольной, называют оптимальным согласованием (рисунок 1.19,б). В качестве таких согласующих цепей могут быть применены, например, LC-цепи лестничного типа, формирующие Чебышевскую (равноволновую) (рисунок 1.19,б) частотную характеристику мощности 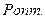
Дата добавления: 2016-02-04; просмотров: 2432;
