Математическое моделирование. Для построения математических моделей в гидравлике могут быть использованы процессы, имеющие единую с гидравликой природу взаимодействия физических тел

Для построения математических моделей в гидравлике могут быть использованы процессы, имеющие единую с гидравликой природу взаимодействия физических тел. Т.е. моделями для процессов, протекающих в жидкостях и газах, могут служить лишь те фи­зические процессы, которые относятся к группе электромагнитных взаимодействий, имеющих одного и того же переносчика взаимодействия - фотон. В таком случае основ­ные процессы, протекающие в модели и натуре, будут иметь одинаковые уравнения, опи­сывающие сходственные процессы.

Так для моделирования гидродинамического поля (поля скоростей движения жидко­сти и газа) могут быть использованы электрическое и тепловое поля.

Из курса физики известны общие уравнения, характеризующие сплошность поля и его изменение. Это известное уравнение неразрывности:

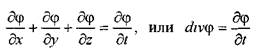
и так называемые уравнения неустановившегося (уравнение Фурье) и установивше­гося (уравнение Лапласа) движения:

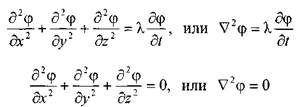
Наиболее удобным для целей моделирования процессов протекающих в жидкостях и газах являются процессы, протекающие в электрическом поле, поскольку последние отли­чаются компактностью, доступностью для измерения и, что самое главное, высокой ско­ростью протекания. Такие особенности электрического поля сделали его популярным для моделирования различных процессов, был разработан специальный аппарат для построе­ния электрических моделей процессов протекающих в жидкостях и газах, - метод электро­гидродинамической аналогии (ЭГДА). Построенные на его базе серийные моделирующие комплексы вплоть до появления цифровых ЭВМ широко использовались в практике на­учных исследований и на прямом производстве. При решении ряда задач актуальность этого метода остаётся поныне.

Модели, строящиеся на базе теплового поля, используются крайне редко из-за тру­доёмкости их создания и реализации.