Некоторые свойства жидкостей

Жидкость – это тело, которое, имея определённый объём, принимает форму сосуда, в котором оно находится.

Свойства жидкостей иногда сходны со свойствами твёрдых тел и газов. К свойствам жидкости относятся:

- малосжимаемость, что имеет сходство с твёрдыми телами;

- относительно высокая плотность;

- ближний порядок в жидкости, что соответствует квазикристаллической или кристаллоподобной структуре. Для жидкости справедливо соотношение вида

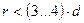. (1.1)

В выражении (1.1):

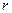- – среднее расстояние между молекулами жидкости;

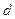- – эффективный диаметр молекулы.

- молекулы жидкости медленно изменяют местоположение внутри жидкости. Согласно Френкелю Я.И. процесс перемещения молекул носит следующий характер. Сначала молекула в течение некоторого времени 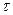совершает колебание в положении равновесия. Затем молекула совершает скачок в другое положение равновесия;

- переохлаждённая жидкость ведёт себя как аморфное тело;

- текучесть.

1.2 Дырочная теория жидкого состояния

Известно, что при плавлении кристалла удельный объём жидкости 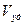увеличивается на 10%. Это происходит потому что под действием отрицательного давления удельный объём жидкости 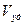равен теоретическому пределу прочности кристалла. В результате большой подвижности частиц в жижкости возникают микроскопические разрывы, называемые микрополостями или дырками. Среднее расстояние между соседними молекулами в жидкости определяется выражением (1.2)

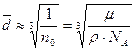. (1.2)

В выражении (1.2):

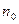- – число молекул в единице объёма жидкости;

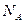- – число Авогадро;

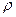- – плотность жидкости;

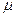- – молярная масса жидкости.

Если в течение некоторого времени 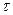молекула совершает колебание в положении равновесия, тогда под временем релаксации 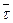будем понимать среднее время «оседлого» пребывания молекулы жидкости в положении равновесия. При повышении температуры жидкости величина времени релаксации будет уменьшаться. Для перехода молекулы от одного положения равновесия к другому необходима энергия активации 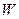. Тогда время релаксации равно

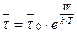. (1.3)

В выражении (1.3):

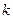- – постоянная Больцмана;

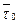- – средний период колебания молекулы в одном положении равновесия.

Если за время 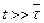действует внешняя сила, то средняя скорость движения молекул в жидкости определяется выражением (1.4):

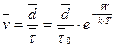. (1.4)

1.3 Давление в жидкости

Упругое свойство жидкости проявляется в том, что отдельные его части действуют друг на друга или на соприкасающиеся с ними тела с силой, зависящей от степени сжатия жидкости. Это воздействие характеризуется физической величиной, называемой давлением.

Считается, что жидкость находится в равновесии, если отдельные её части не перемещаются друг относительно друга или относительно граничащих с ними тел. При нахождении жидкости в равновесии соприкасающиеся по площадке 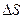части жидкости действуют друг на друга с силами равными по величине и противоположными по направлению. Таким образом, как показано на рисунке 1.1, равнодействующая всех сил 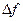, действующих на площадку 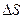, направлена по нормали к этой площадке.

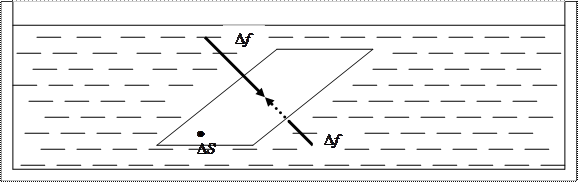Рисунок 1.1 – Сечение сосуда с жидкостью, находящейся в равновесии

Тогда давление жидкости определяется как

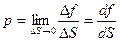. (1.5)

Давление 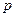– скалярная величина. Единицей измерения давления в системе «СИ» является ньютон на метр в квадрате [Н/м²]. Часто используется другая единица измерения – паскаль [Па]. Один паскаль соответствует одному ньютону на метр в квадрате.

Существуют другие единицы измерения давления:

- техническая атмосфера (ат), что соответствует одному килограмму силы на сантиметр в квадрате [кгс/см²];

- физическая атмосфера (атм), что соответствует атмосферному давлению 760 миллиметров ртутного столба [мм рт. ст.].

Соотношения между технической и физической атмосферами следующие:

;

.

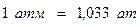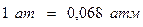1.4 Распределение давления в покоящейся жидкости

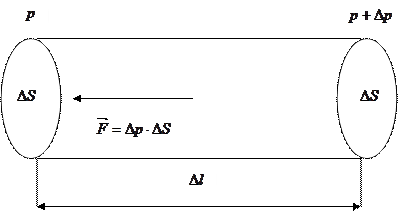Выделим в жидкости небольшой произвольно ориентированный цилиндрический объём высотой 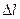и основанием 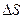, как показано на рисунке 1.2.

Рисунок 1.2 – Цилиндрический объём жидкости высотой 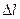и основанием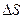

Разность давлений 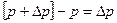порождает силу 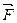, действующую в направлении снижения давления. По этой же причине в этом же направлении жидкость пришла бы в движение. Если разности давления нет, т.е 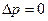, то в любой точке жидкости из-за постоянства давления должно выполняться условие .

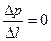Рассмотрим распределение давления в жидкости при наличии объёмных сил. При горизонтальном расположении цилиндра (рисунок 1.3 «а») объёмная сила направлена по вертикали, а вдоль оси цилиндра действуют силы 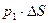и . И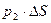з условия равновесия следует, что 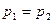, т.е. во всех точках жидкости, лежащих на одном уровне (в горизонтальной плоскости) давление постоянно.

При вертикальном расположении цилиндра (рисунок 1.3 «б») объёмная сила направлена вертикально вниз. Вдоль оси действуют следующие силы:

- ;

- ;

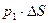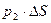- объёмная сила равная 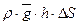. Здесь 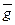– вектор ускорения свободного падения.

а)

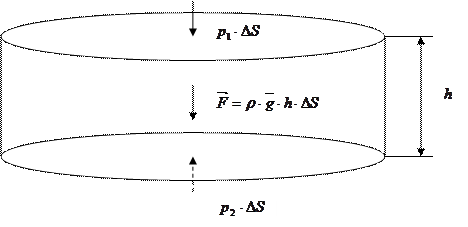б)

Рисунок 1.3 – Цилиндрический объём жидкости, имеющий расположение а) горизонтальное, б) вертикальное

Условие равновесия при вертикальном расположении цилиндра имеет вид:

.

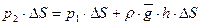Сокращая левую и правую части выражения на величину 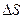, получаем условие равновесия в окончательном виде:

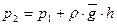. (1.6)