Свойства линейной мерной единицы R
Длина R (после выбора её частного значения) принимается обоюдно зависимая:
1. от длины луча состоящего из отрезков R , 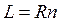
2. от составляющих длину R точечных отрезков T,
где Т – отрезок полученный из 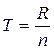
Общая зависимость принимается следующая:
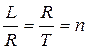
где линейная мерная единица R состоит из n «количества» точечных отрезков T
где луч L состоит из n «количества» мерных отрезков R .
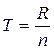
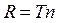
Определимся с линейной продолжительностью трехмерного пространства:
Геометрический луч – есть полупрямая.
(прямая состоит из двух лучей).
Длина оси 0X , в одном направлении это луч
(в обоих направлениях – прямая).
Длина геометрического луча L равна произведению мерной единицы R на количественное значение n .
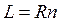
Значение n - может трактоваться не только как стремящееся к бесконечности количественное значение.
Для решения частных задач, не зависящих от продолжительности геометрического луча, значение n - может трактоваться как достаточно большое число.
Принимая исходный формат 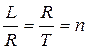
мы тем самым форматируем все без исключения пространственные величины. Выглядит это так:
Длина геометрической прямой E- равна сумме длин составляющих её лучей.
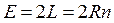
Где 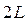 есть длина прямой, выраженная в длинах луча,
есть длина прямой, выраженная в длинах луча,
Где 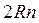 есть длина прямой, выраженная в мерных единицах (отрезках длины R).
есть длина прямой, выраженная в мерных единицах (отрезках длины R).
Так же длину прямой мы можем выразить в точечных отрезках T ,
Тогда E будет иметь вид: 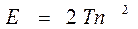
Мировая линия E (геометрическая прямая имеющее сечение 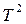 (квадрат со сторонами Т))
(квадрат со сторонами Т))
Длина мировой линии 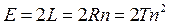
Объем мировой линии  (начального сечения
(начального сечения  ),
),
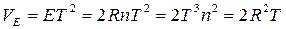
Мировой луч– геометрический луч, имеющий начальное сечение 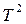
Длина мирового луча
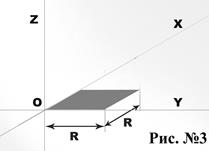
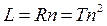
Объем мирового луча:
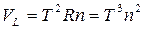
Дата добавления: 2016-02-04; просмотров: 616;
