Форматирование трехмерного пространства.

( приведение всех линейных и объемных величин пространства, а так же объектов в нем содержащихся, к единой системе мер.)

Форматирование трехмерного пространства позволяет уверенно, без каких либо противоречий, парадоксов и неопределенностей, оперировать бесконечно большими и бесконечно малыми величинами.

Из неоспоримой подтвержденной информации (не зависимой, от каких либо субъективных теоретических построений) современная наука располагает равномерностью распределения материи на макро уровне.

( данный факт общеизвестен и признан официальной наукой как достоверный).

Данная равномерность распределения материи зафиксирована в системе мер (координат, эталонов) соответствующей реальной версии трехмерного пространства.

Для основных теоретических построений в качестве пространственной схемы используем реальное пространство.

В качестве объемной шкалы используется Декартовая система координат.

Используемые обозначения:

R - линейная мерная единица.

Линейная мерная единица R - произвольным образом выбранная линейная величина, в дальнейшем являющееся единственной линейной мерной базой для всех (больших и малых) расстояний в реальном пространстве (выбирается одновременно для всех дальнейших вычислений).

( для наглядности R можно принять равной некому количеству, например километров )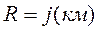

n - неконечный количественный показатель в базовом случае трактуется как неконечное количественное значение.

В частном случае неконечный количественный показатель n - может трактоваться и использоваться (как конечный количественный показатель) как достаточно большое число.

Неконечный количественный показатель n - логический аналог количественного выражения стремящейся к бесконечности переменной величины ( в обывательском смысле – бесконечность ( ∞ ).

L - геометрический луч (длина геометрического луча). Луч – линейная величина, замкнутая с одной стороны.

Определимся с трактовкой длины L геометрического луча:

К данному вопросу возможны два похода:

Подход первый:

Длина луча принимается как теоретическая модель, состоящая из незамкнутой совокупности безразмерных точек (общеизвестная «наивная» интеллектуально несостоятельная трактовка).

Подход второй:

Длина луча принимается как незамкнутая совокупность калиброванных линейных величин(отрезков).

Длина любого отрезка принимается как совокупность мельчайших отрезков, имеющих длину не равную нулю.

Воспользуемся подходом №2.

В данном подходе в качестве базы луча принимается линейная мерная единица R (некий отрезок определенной длины).

Длина самого луча при данном подходе принимается равной произведению мерной единицы R и неконечного количественного показателя n.