ИЗУЧЕНИЕ РЕЖИМОВ ТЕЧЕНИЯ ЖИДКОСТИ

В КРУГЛОЙ ТРУБЕ (ОПЫТЫ О. РЕЙНОЛЬДСА)

В первой половине XIX века немецкий инженер Г. Хаген, а в 1880 г русский ученый Д. И. Менделеев обратили внимание на существование разных режимов движения жидкости. В 1883 г английский физик О. Рейнольдс провел экспериментальные исследования, в которых наглядно показал наличие двух режимов движения жидкости.

В отличие от движения твердого тела как единого целого течение легкоподвижной жидкости (газа) сопровождается внутренними перемещениями ее частиц, имеющих большое число степеней свободы.

Различают два режима течения жидкости: слоистый, упорядоченный или ламинарный (от латинского слова lamina-слой, пластинка) и турбулентный (turbulentus-вихревой). Ламинарный поток имеет слоистый характер - частицы жидкости движутся с различными скоростями параллельно оси трубы без перемешивания. Касательные напряжения, возникающие между параллельными слоями жидкости, обусловлены ее вязкостью и подчиняются закону внутреннего трения Ньютона, который имеет вид

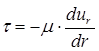, (4.1)

где 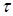- касательное напряжение; 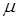- динамическая вязкость жидкости; 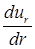- градиент скорости.

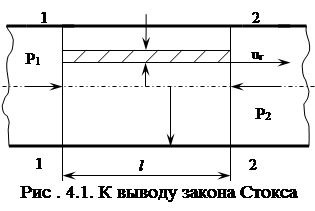Рассмотрим движение вязкой жидкости в круглой трубе радиусом R при установившемся ламинарном режиме. Выделяя в потоке цилиндрический объем жидкости длиной l и произвольным радиусом r (рис. 4.1), из условия динамического равновесия получим, что разность сил давления, приложенных к выделенному объему в сечениях 1-1 и 2-2, уравновешивается силами трения, возникающими на его боковой поверхности

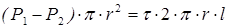, 4.2)

где Р₁ и Р₂ –давление в центрах сечений 1-1 и 2-2.

Из уравнения энергетического баланса напоров для рассматриваемого случая, следует, что потери на трение по длине определяются зависимостью

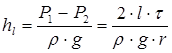(4.3)

Из выражения (4.3) следует, что касательные напряжения в сечении потока распределяются линейно

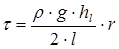(4.4)

Решая совместно (4.4) и (4.1), получаем дифференциальное уравнение, определяющее скорость u_r как функцию радиуса r

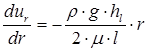(4.5)

Интегрируя уравнение (4.5) с учетом граничного условия (u_r = 0 при R = r) получаем параболический закон распределения скоростей (рис. 4.2) по сечению круглой трубы

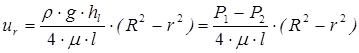(4.6)

Скорость имеет максимальное значение на оси трубы, когда r = 0

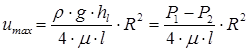(4.7)

Сопоставляя зависимости (4.6) и (4.7), находим закон Стокса, выражающий параболическое распределение скоростей в сечении трубопровода при ламинарном движении

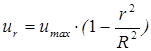(4.8)

Подсчитав расход жидкости суммированием расходов через элементарные кольцевые площадки толщиной dr (рис.4.1) сечения потока, находится средняя скорость

			umax

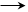
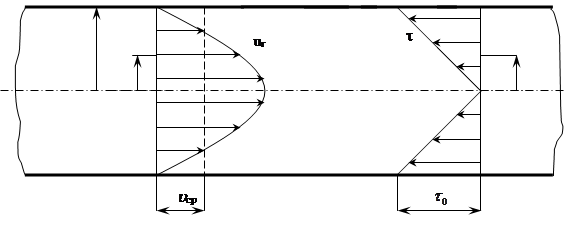Рис. 4.2. Распределение скоростей и касательных напряжений

по сечению ламинарного потока в круглой трубе

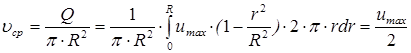(4.9)

Из (4.9) следует, что средняя скорость потока при ламинарном режиме равна половине максимальной.

Расход жидкости в круглой трубе при ее ламинарном движении определяется уравнением Пуазейля

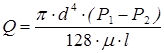, (4.10)

где d – внутренний диаметр трубы.

Турбулентный поток характеризуется беспорядочным, хаотическим движением частиц жидкости. Наряду с основным поступательным перемещением жидкости вдоль трубы наблюдаются незакономерные поперечные перемещения и вращательные движения частиц, которые приводят к интенсивному перемешиванию жидкости. Вследствие интенсивного вихреобразования частицы жидкости при турбулентном движении описывают весьма сложные траектории, а местные скорости не сохраняются постоянными даже в том случае, когда расход потока постоянен во времени. Таким образом, установившегося движения (в строгом понимании) в турбулентном потоке не существует. Измерения показывают, наоборот, что в каждой точке скорость непрерывно меняется как по величине, так и по направлению. Поэтому скорость в точке турбулентного потока называют мгновенной местной скоростью.

Раскладывая мгновенную скорость на три взаимно перпендикулярных направления, получим продольную составляющую u_x, направленную по нормали к живому сечению, и две поперечные составляющие u_y и u_z, лежащие в плоскости живого сечения потока. Как продольные, так и поперечные составляющие мгновенной скорости все время меняются. Изменение во времени проекции мгновенной местной скорости на какое-либо направление называется пульсацией скорости. С помощью чувствительных приборов можно наблюдать пульсации скоростей и записать их хронограмму.

Для данной точки осредненная во времени скорость u_x находится из соотношения

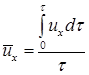(4.11)

Таким образом, величина 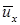равна высоте прямоугольника, равновеликого площади, заключенной между пульсационной кривой и осью абсцисс в пределах изменения времени от 0 до t (рис. 4.3).

Разность между истинной и осредненной скоростями называется мгновенной пульсационной скоростью и обозначается Du (индекс x здесь и далее опускаем)

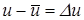(4.12)

Согласно рис. 4.3, величина Du имеет переменный знак, поэтому

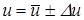(4.13)

Понятие осредненной скорости 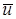не следует путать с понятием средней скорости u. Последняя представляет собой не среднюю во времени скорость в данной точке, а скорость, осредненную для всего поперечного сечения трубопровода.

Таким образом, осреднение скоростей во времени позволяет приближенно считать турбулентное движение стационарным. В этом смысле оно может рассматриваться как квазистационарное.

Интенсивность турбулентности выражают отношением

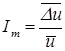, (4.14)

где 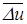- среднее квадратичное значение пульсационной скорости, с помощью которого осредняются во всех направлениях мгновенные пульсационные скорости по их абсолютной величине.

Интенсивность турбулентности является мерой пульсаций в данной точке потока. При турбулентном течении по трубам I_m»0,01¸0,1.

Если средние пульсации скорости одинаковы по всем направлениям, то такая турбулентность называется изотропной.

Помимо интенсивности I_m другими важными характеристиками турбулентного движения являются масштаб турбулентности и турбулентная вязкость n_т.

Чем ближе друг к другу находятся две частицы жидкости в турбулентном потоке, тем более близки их истинные (мгновенные) скорости. В то же время у достаточно удаленных одна от другой частиц совсем нет связи между колебаниями или пульсациями их скоростей. Достаточно близко расположенные частицы, движущиеся совместно, можно считать принадлежащими к некоторой единой совокупности, называемой обычно вихрем. Размер таких вихрей, или глубина их проникания до разрушения, которая приближенно может быть отождествлена с расстоянием между двумя ближайшими частицами, уже не принадлежащими к одному вихрю, зависит от степени развития турбулентности в потоке, или ее масштаба, и поэтому носит название масштаба турбулентности.

Турбулентная вязкость, в отличие от обычной вязкости, не является физико-химической константой, определяемой природой жидкости, ее температурой и давлением. Турбулентная вязкость зависит от скорости жидкости и других параметров обусловливающих степень турбулентности потока (в частности, расстояния от стенки трубы и т.д.).

Различный характер движения жидкостей при ламинарном и турбулентном режимах приводит и к неодинаковым потерям напора (энергии). При турбулентном режиме вследствие перемешивания и соударения эти потери больше, чем при ламинарном. Так, если потери напора в ламинарном потоке пропорциональны средней скорости в первой степени, то в турбулентном потока – средней скорости в степени, изменяющейся от 1,75 до 2,0.

Многочисленными исследованиями с разными жидкостями при различных скоростях и размерах потока установлено, что на режим движения жидкости оказывают влияние ее вязкость m, плотность r, характерный линейный размер потока l и средняя скорость u. Исходя из теории подобия, эти параметры объединяются в безразмерный комплекс Re, названный числом Рейнольдса, который для круглой трубы диаметром d, имеет вид

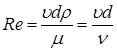(4.15)

Если сечение потока некруглое, то в качестве характерного линейного размера l часто применяется отношение площади S живого сечения к смоченному жидкостью периметру П, называемое гидравлическим радиусом r_г=S/П. Очевидно, r_г линейная величина. В частном случае круглого сечения r_г=d/4, т.е. d=4 r_г. Так как r_г можно вычислить для сечения любой сложной формы, то последнее соотношение распространяется и на сечения некруглой формы. При этом величина d называется эквивалентным диаметром и обозначается d_э. Таким образом, для сечения некруглой формы в качестве l может быть принят также и эквивалентный диаметр.

Число Рейнольдса Re представляет меру отношения сил инерции к силам трения, действующим в движущейся жидкости. В зависимости от указанного соотношения устанавливается или ламинарный, или турбулентный режим движения.

Переход от ламинарного к турбулентному движению характеризуется критическим значением Рейнольдса и обозначается Re_кр. Так, при движении жидкостей по прямым гладким трубам Re_кр= 2320. При Re < 2320 течение обычно является ламинарным, поэтому данную область значений Re называют областью устойчивого ламинарного режима течения. При Re > 2320 чаще всего наблюдается турбулентный характер движения. Однако при 2320 < Re < 10000 режим течения еще неустойчиво турбулентный (эту область изменения значений Re часто называют переходной). Лишь при Re > 10000 турбулентное движение становится устойчивым (развитым).

Следует отметить, что Re_кр зависит от целого ряда факторов, например, от условий входа потока в трубопровод (плавного или резкого и т.д.) и наличия в нем начальных возмущений, определяемых обстоятельствами движения потока перед входом в рассматриваемую трубу (или, как говорят, "историей потока"). Поэтому число Re_кр может в зависимости от указанных факторов меняться в широких пределах (достигнуты в особых условиях числа Re_кр, равные, например, 50000). Чем хуже условия входа (острые края трубы и т.д.) или чем более возмущен поток на входе, тем меньше при прочих равных условиях число Re_кр. Однако критические значения чисел Рейнольдса не зависят от рода жидкости, диаметра трубы, шероховатости ее стенок. Например, для воздуха, воды, масла и других жидкостей Re_кр будет в данных граничных условиях одинаковым.

Цель работы – установить опытным путем наличие двух режимов движения жидкости, изучить их структуру и на основании экспериментальных данных рассчитать критические значения числа Рейнольдса.