ИССЛЕДОВАНИЕ УСТАНОВИВШЕГОСЯ ДВИЖЕНИЯ ГАЗА В ТРУБОПРОВОДЕ ПЕРЕМЕННОГО СЕЧЕНИЯ

Установившимся называется такое движение жидкости (газа), при котором скорость и давление в любой ее фиксированной точке не изменяются во времени. В условиях такого движения жидкости значения массового расхода G в любом сечении трубопровода остается неизменным. Эта закономерность учитывается с помощью уравнения расхода (неразрывности), которое имеет вид

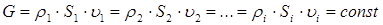, (5.1)

где 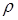- плотность жидкости, кг/м³; 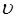- средняя скорость движения жидкости, м/с; S – площадь живого (поперечного) сечения, м².

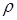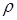Считая жидкость практически несжимаемой, т.е. ₁= ₂=…= 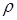_i= const, величина объемного расхода Q также не изменяется, а именно

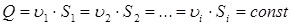(5.2)

На основании уравнения неразрывности (5.2) определяется средняя скорость 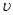в любом i-ом живом сечении потока

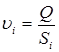(5.3)

Одним из основных уравнений гидравлики, используемых при решении многих практических задач, является уравнение Д. Бернулли, которое получается интегрированием уравнений Л. Эйлера при движении жидкости под действием силы тяжести. Уравнение Д. Бернулли является (применительно к потоку жидкости) выражением закона сохранения энергии, которое связывает потенциальную (mgz) и кинетическую (mu²/2) энергии частицы жидкости массой m в двух ее положениях с работой внешних сил давления (mgР/rg) и сил сопротивления (mgh_п).

Составление баланса энергии массы реальной жидкости m=1, проходящей через два произвольные живые сечения 1-1 и 2-2 (рис. 5.1) элементарной струйки (скорости частиц жидкости по живому сечению струйки одинаковы) приводит к уравнению Д. Бернулли для элементарной струйки, которое имеет вид

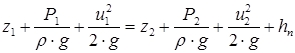(5.4)

Уравнение (5.4) в целом и входящие в его слагаемые следует интерпретировать с геометрической и энергетической точек зрения. С геометрической точки зрения (рис. 5.1): z-высота положения (геометрический напор) - расстояние от центра тяжести живого сечения до плоскости сравнения 0-0, которая выбирается произвольно, так как разность (z₁-z₂) не зависит от ее положения;

Р/rg - пьезометрическая высота - высота такого столба жидкости (плотностью 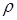), который у своего основания создает давление Р, равное давлению в рассматриваемом сечении;

u²/2g - скоростной напор - высота, с которой должно упасть тело массой m=1, чтобы в конце пути приобрести скорость u.

z + Р/rg - гидростатический напор;

z + Р/rg + u²/2g - гидродинамический или полный напор.

Индексами 1 и 2 обозначены величины, относящиеся соответственно к первому и второму живым сечениям потока. Член h_п, входящий в уравнение (5.4), показывает величину изменения или потери полного напора между рассматриваемыми сечениями.

С энергетической точки зрения:

z - удельная (отнесенная к единице веса) энергия положения жидкости в рассматриваемом сечении;

Р/rg - удельная энергия давления;

u²/2g - удельная кинетическая энергия;

z + Р/rg - условно называется удельной потенциальной энергией;

z + Р/rg + u²/2g - полная удельная энергия жидкости;

h_п - потери удельной энергии жидкости между рассматриваемыми сечениями.

Таким образом, согласно уравнению Д. Бернулли следует, что по длине струйки реальной жидкости гидродинамический напор (полная удельная энергия) уменьшается. Кроме того, из данного уравнения вытекает также, что по длине потока с ростом давления (пьезометрического напора) скорости уменьшаются и, наоборот, с увеличением скорости давление падает.

Обычно дают графическую интерпретацию уравнения Д. Бернулли, которая изображается в виде диаграммы.

Для построения диаграммы уравнения Д. Бернулли от произвольно выбранной плоскости сравнения 0-0 (рис. 5.1) откладывают вверх ординаты z и получают очертание оси струйки. Затем от оси струйки откладывают вверх значения пьезометрических высот и получают линию П-П, которая называется пьезометрической линией. Расстояние от пьезометрической линии до плоскости сравнения указывает, в каком сечении струйки величину гидростатического напора z + Р/rg (величину удельной потенциальной энергии). Откладывая далее вверх от пьезометрической линии значения скоростного напора u²/2g, получают линию гидродинамического напора Е-Е, расстояние от которой до плоскости сравнения 0-0 дает значение гидродинамического напора (полной удельной энергии) в соответствую-щих сечениях элементарной струйки (рис.5.1).

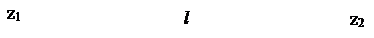
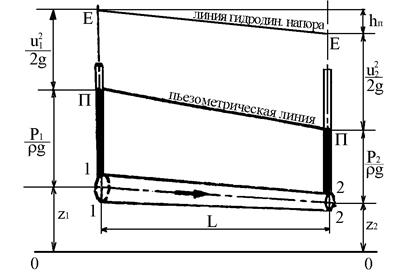
Рис.5.1. Геометрическая и энергетическая интерпретация

уравнения Д. Бернулли

Отношение потери гидродинамического напора (потери удельной энергии) на единицу длины струйки, на которой они произошли, называется гидравлическим уклоном. Гидравлический уклон - величина безразмерная и в общем случае переменная. Обычно его обозначают буквой i_l. Гидравлический уклон в данном сечении выражается зависимостью

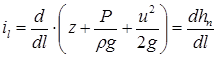(5.5)

Понятие об уклоне вводится и для пьезометрической линии, который показывает изменение пьезометрического напора на единицу длины

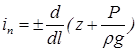(5.6)

Величина i_г= 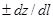называется геометрическим уклоном и характеризует наклон оси струйки.

В отличие от гидравлического уклона i_l , имеющего всегда положительное значение, i_п и i_г могут быть положительными, равными нулю, и отрицательными.

Переходя к рассмотрению уравнения Д. Бернулли для потока реальной жидкости, необходимо отметить одну особенность. Скорости по сечению потока реальной жидкости, состоящего из множества элементарных струек, неодинаковы. Их распределение подчиняется определенным законам. В отношении уравнения Д. Бернулли неодинаковость скоростей по живому сечению потока приводит к тому, что кинетическая энергия, вычисленная по средней скорости в данном сечении 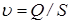, не равна кинетической энергии, вычисленной как сумма энергий всех элементарных струек, составляющих поток и имеющих разные скорости.

С учетом вышеизложенного уравнение Д. Бернулли для потока реальной жидкости записывается в виде

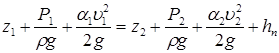(5.7)

В уравнении (5.7) z и Р/rg имеют такой же смысл, как и в уравнении Д. Бернулли для элементарной струйки.

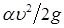- среднее значение удельной кинетической энергии в соответствующем сечении потока; h_п - величина потерь удельной энергии между сечениями.

Уравнения (5.7) и (5.4) отличаются тем, что в (5.7) скоростной напор, определяемый средней скоростью, дополнен коэффициентом 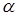, носящим название коэффициента Кориолиса. Он характеризует отношение кинетической энергии потока в данном живом сечении к кинетической энергии, вычисленной в предположении, что скорости во всех точках сечения одинаковы и равны средней 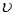. Величина этого коэффициента зависит от степени неравномерности распределения скорости по сечению. Коэффициент Кориолиса всегда больше единицы (за исключением случая, когда местные скорости в данном сечении равны между собой, тогда 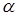=1).

Для большинства инженерных расчетов (например, при расчете трубопроводов) можно полагать 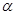=1, тогда уравнение Д. Бернулли для потока реальной жидкости имеет вид

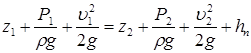(5.8)

Цель работы- в условиях установившегося потока газа (воздуха) в трубопроводе переменного сечения определить пьезометрическое, скоростное и полное давление в заданных сечениях, а также построить диаграмму уравнения Д. Бернулли.

Описание установки

Лабораторная установка (рис 5.2) состоит из подводящего трубопровода 1 с участком переменного сечения 2, отводящего трубопровода 3, центробежного вентилятора 4, автотрансформатора 5, батарейного вакуумметра 6 и вакуумметров 7 В₁, В₃ и В₆ для измерения полного напора соответственно в сечениях 1, 3 и 6 (рис. 5.2).

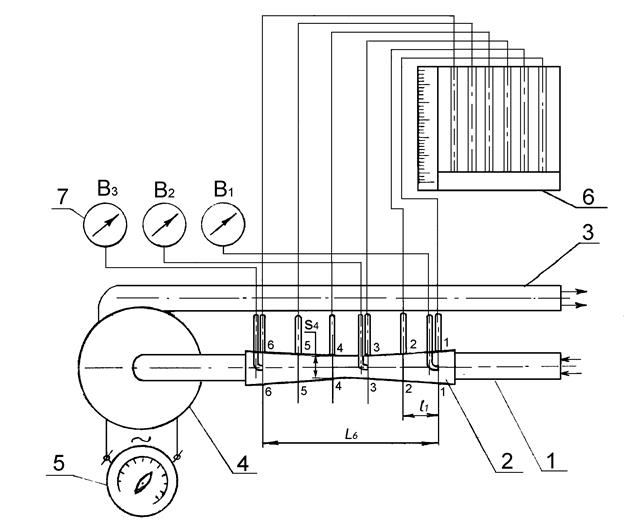
Рис. 5.2. Схема экспериментальной установки для исследования движения воздуха в трубопроводе переменного сечения

Чаша батарейного вакуумметра 6 заполняется водой до соответствующей отметки на корпусе. Пьезометрический напор измеряется в каждом сечении трубопровода (сечения 1-6) с помощью батарейного вакуумметра 6, подключенного гибкими трубками к отверстиям в соответствующих сечениях. В сечениях 1, 3 и 6 установлены изогнутые трубки (трубки Пито) для измерения полного напора, которые подключены к соответствующим вакуумметрам В₁, В₃ и В₆ (рис. 5.2).