ЛЕКЦИЯ 8. ПРИНЯТИЕ ТЕХНИЧЕСКИХ РЕШЕНИЙ
При проектировании новых технических систем (изделий) и при совершенствовании существующих очень часто приходится принимать решения, не имея достаточной информации, иными словами, в условиях неопределенности. Для обоснованного принятия решений в таких случаях применяют специальные математические методы.
В некоторых простых ситуациях эти методы дают возможность фактически найти оптимальное решение; в более сложных случаях дают дополнительный материал (информацию для размышления), позволяющий глубже разобраться в сложной обстановке и оценить преимущества и недостатки каждого варианта с различных точек зрения.
Методами обоснования решений в условиях неопределенности занимаются математическая теория игр.
В теории игр рассматриваются такие ситуации, когда имеются два участника выполнения операции, каждый из которых преследует различные и противоположные цели. В качестве участников могут выступать целые коллективы.
Такие случаи могут встретиться при проектировании между конструкторами и технологами, на производстве между технологическим и ремонтным персоналом.
Во всех случаях предполагается, что операция проводится против разумного противника, преследующего свои собственные цели и оказывающего сознательное противодействие достижению цели первой стороной.
Какие именно действия предпримет конкурент, заранее не известно, но можно уверенно предполагать, что он не сделает ничего такого, чтобы было невыгодно ему самому.
Так как цели противоположны, а результат мероприятия каждой из сторон зависит от того, какие действия предпримет конкурент, их называют конфликтными ситуациями.
Каждая взятая непосредственно из практики конфликтная ситуация очень сложна, и ее анализ затрудняется наличием многочисленных несущественных факторов. Чтобы сделать возможным математический анализ конфликтной ситуации, отвлекаются от всех второстепенных и малозначащих факторов и строят упрощенную, схематизированную модель. Такую модель и называют игрой.
Возможные варианты игры сводят в прямоугольную таблицу, называемую платежной матрицей. Строки платежной матрицы соответствуют различным стратегиям игрока А, а столбцы - стратегиям игрока В. Величина qij на пересечении соответствующих строк и столбцов называется ценой игры:
| B1 | B2 | ... | Bn | |
| A1 | q11 | q12 | ... | q1n |
| A2 | q21 | q22 | ... | q2n |
| ... | .... | .... | ... | ... |
| Am | qm1 | qm2 | ... | qmn |
Целью теории игр является выработка рекомендаций для разумного поведения игроков в конфликтной ситуации, т.е. указание оптимальной стратегии для каждого из них.
Для нахождения оптимальной стратегии необходимо проанализировать все возможные стратегии и рассчитывать на то, что разумный противник на каждую из них будет отвечать такой, при которой выигрыш игрока А минимален. Т.е. игрок В будет стремиться уменьшить выигрыш игрока А, а игрок А будет стремиться увеличить проигрыш игрока В.
Минимальные числа в каждой строке обозначаются ai и выписываются в виде добавочного столбца платежной матрицы:
| B1 | B2 | ... | Bn | ai | |
| A1 | q11 | q12 | ... | q1n | a1 |
| A2 | q21 | q22 | ... | q2n | a2 |
| ... | .... | .... | ... | ... | ... |
| Am | qm1 | qm2 | ... | qmn | am |
| bj | b1 | b2 | ... | bn |
В каждой строке будет свое ai = min qij. Предпочтительной для игрока А является та стратегия, при которой ai обращается в максимум, т.е. a=maxai или, принимая во внимание предыдущее выражение, a=mах min qij.
Величина a называется максиминным выигрышем или просто макси-мином, а соответствующая ей стратегия — максиминной стратегией. Если придерживаться максиминной стратегии, то при любом поведении стороны В гарантирован выигрыш, во всяком случае не меньший a.
Поэтому a называют также нижней ценой игры - это тот гарантированный минимум, который можно обеспечить при наиболее осторожной (перестраховочной) стратегии.
Очевидно, что аналогичные рассуждения можно провести и для стороны В. Эта сторона должна рассмотреть все свои стратегии, выделяя для каждой из них максимальные значения выигрыша: bj = max qjj. Эти значения выписываются в дополнительной строке платежной матрицы. Из всех значений bj находится минимальное:
b = min max qij .
Величина b дает минимаксный выигрыш, или просто минимакс. Стратегия, соответствующая b, называется минимаксной.
Придерживаясь этой стратегии, сторона В гарантирована, что в любом случае проиграет не больше b. Поэтому b называют также верхней ценой игры.
Предположение о разумности каждого игрока приводит к тому, что они должны выбирать соответствующие "осторожные" максиминные и минимаксные стратегии. Этот принцип осторожности получил название принципа минимакса.
Особое место занимают игры, для которых
min max qij = max min qij,
т.е. нижняя цена игры равна верхней a = b = u. Величина v называется чистой ценой игры. В платежной матрице такой игры существует элемент, который одновременно является минимальным в своей строке и максимальным в своем столбце.
Этому элементу соответствует пара минимаксных стратегий, которые будут оптимальными для обоих игроков, поскольку любое отклонение от этих стратегий приводит к уменьшению выигрыша первого игрока и увеличению проигрыша второго по сравнению с ценой игры.
Очень острой бывает ситуация и при разработке новой техники и внедрении современных технологий. Одну из таких задач рассмотрим на примере.
Пример. Конструктор получил задание разработать определенное изделие. После длительного размышления он пришел к выводу, что задание может быть выполнено в виде одного из трех возможных вариантов: K1, K2, K3. Кроме того, каждый вариант может быть реализован каким-либо из трех технологических процессов: Т1, Т2, Т3. Предположим для простоты, что параметры изделия во всех случаях будут практически одинаковыми, но внешний вид изделий различен.
Если первый конструктивный вариант K1 будет реализован с помощью первого технологического процесса, то внешний вид устройства окажется наилучшим и оценивается экспертами в 9 баллов. Этот же конструктивный вариант при реализации вторым технологическим процессом Т2 оценивается в 6 баллов, а третьим в 5. Конструктивный вариант K2 при реализации технологическим процессом Т1 приводит к оценке 8 баллов, а при втором и третьем технологических процессах оценивается одинаково — 7 баллов. Для варианта K3 соответствующие оценки будут 7, 5 и 8 баллов.
Конфликтная ситуация возникает из-за того, что затраты на реализацию каждого конструктивно-технологического варианта не одинаковы. Для простоты расчетов и наглядности допустим, что затраты пропорциональны оценке внешнего вида, т.е. вариант, имеющий наибольшую оценку, оказывается и самым дорогим.
Конструктору надо выбрать и представить на утверждение только один вариант. Конечно, ему хочется взять самый красивый, но он отлично понимает, что после того, как он представит избранный вариант, найдутся сторонники реализации аппаратуры с наименьшими затратами, даже если это будет в ущерб внешнему виду. Назовем такую группу условно "экономистами", хотя для конструктора это как раз и есть противоборствующая сторона, мешающая ему создать совершенное изделие.
Очередная задача конструктора - так выбрать конструктивный вариант, чтобы обеспечить, если не самый лучший, то во всяком случае оптимальный как с точки зрения внешнего вида, так и стоимости. Для решения такой проблемы можно использовать игровые методы. Сведем все данные в единую матрицу игры (табл. 8.1).
Таблица 8.1 - Матрица игры для конструктивного и технологических вариантов
| Конструктивный вариант | Технологический вариант | ||
| Т1 | Т2 | Т3 | |
| K1 | |||
| K2 | |||
| K3 |
Если конструктор выберет вариант К1, то экономисты будут настаивать на технологии Т3 и получится изделие, внешний вид которого оценивается в 5 баллов. На вариант К2 ответ будет Т2 или Т3, так как оба они приводят к одинаковым затратам и дают равноценный результат, оцениваемый в 7 баллов. На вариант К3 реакция экономистов будет Т2, дающая 5 баллов. Очевидно, что, с точки зрения конструктора, преимущество имеет конструктивный вариант К2, так как даже при неблагоприятных обстоятельствах получится изделие, оцениваемое в 7 баллов (выигрыш 7), а может быть даже 8, если удастся уговорить экономистов на технологический вариант Т1.
Встанем теперь на позицию экономистов (нашего разумного противника) и посмотрим, какой технологический процесс для них наиболее выгоден с точки зрения снижения затрат. Если выбрать Т1, то при конструктивном варианте К1 затраты окажутся наибольшими - 9. При варианте Т2 может быть вариант К2 с затратами 7, а при Т3 - конструктивный вариант К3, требующий затрат 8. Таким образом, для экономистов оптимальным является технологический процесс Т2, поскольку он потребует меньших затрат при различных конструктивных вариантах. Следовательно, в данном примере стратегия К2 Т2 с выигрышем 7 является наиболее выгодной сразу для обеих сторон - максимальный выигрыш К совпадает с минимальным проигрышем Т.
При поиске решений в технике часто использует некоторые методы из теории принятия решений.
В общем случае считается, что имеется несколько вариантов решений (мероприятий) Ei, которые могут быть реализованы в различных условиях (состояниях) объекта (или системы) Fj. Результат реализации варианта Ei в условиях Fj можно охарактеризовать с помощью значения оценочной функции eij. В качестве eij может выступать экономический эффект (прибыль, затраты) или один из показателей надежности.
Для представления возможных результатов решений используется матрица решений 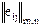 , где m – количество вариантов решения; n – количество состояний (условий).
, где m – количество вариантов решения; n – количество состояний (условий).
Принятие решений представляет собой выбор одного из некоторого множества рассматриваемых вариантов EiÎE (i = 1..m). Каждому варианту решения вследствие различных внешних условий (состояний) Fj соответствует некоторый результат eij.
Выбор наилучшего варианта решения 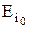 осуществляется с помощью критериев Z. Существуют различные критерии выбора. Рассмотрим некоторые из них (таблица 8.2).
осуществляется с помощью критериев Z. Существуют различные критерии выбора. Рассмотрим некоторые из них (таблица 8.2).
Также можно использовать критерии:
а) позиция компромисса между оптимистическим и пессимистическим подходами
 ,
,
т.е. выбирается наибольшее значение из комбинаций наибольшего и наименьшего результата для каждого варианта Ei;
б) оптимистическая позиция – выбор наибольшего из всех возможных результатов
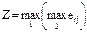 ;
;
в) позиция нейтралитета – наибольшее из средних результатов
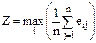 .
.
Таблица 8.2 – Критерии принятия решений
| Наименование | Целевая функция | Примечания, условия применения |
| 1.Минимаксный критерий (ММ) |
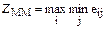
| Позиция крайней осторожности (пессимизма). Риск полностью исключается. Какие бы состояния Fj не встретились, соответствующий результат не может оказаться хуже ZMM. Условия применения: 1) ничего не известно о возможности появления внешних состояний Fj; 2) приходится считаться с появлением различных внешних состояний Fj; 3) решение реализуется один раз; 4) необходимо исключить риск |
| 2. Критерий Байеса-Лапласа (BL) |
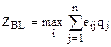 ,
где qj – вероятность появления внешнего состояния Fj ; ,
где qj – вероятность появления внешнего состояния Fj ;
| Оптимистичнее, чем ММ-критерий. Предполагает более высокий уровень информативности. Условия применения: 1) вероятности появления состояний Fj известны и не зависят от времени; 2) решение реализуется бесконечно много раз; 3) для малого числа реализаций решения допустим некоторый риск |
| 3. Критерий Сэвиджа (S) |
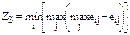
| Позиция относительного пессимизма. Минимизация максимально возможных потерь. Условия применения: 1) состояния оказывают одинаковое влияние на решение; 2) ничего не известно о возможности появления внешних состояний Fj; 3) решение реализуется один раз; 4) необходимо исключить риск |
| 4. Критерий Гурвица (HW) |
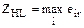 , ,
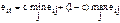 ,
где c – весовой множитель, чаще всего c=0.5 ,
где c – весовой множитель, чаще всего c=0.5
| Позиция между крайним оптимизмом и пессимизмом. Наибольшая средневзвешенная величина наименьшего и наибольшего результата. Условия применения: 1) о вероятностях появления состояний Fj ничего не известно; 2) с появлением состояний Fj необходимо считаться; 3) реализуется лишь малое количество решений; 4) допускается некоторый риск |
Продолжение таблицы 8.2
| 5. Критерий Гермейера (G) |
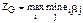
| Ориентирован на величину потерь. Решения – эффективные и пригодные к компромиссу. Условия применения: 1) вероятности появления состояний Fj известны; 2) с появлением тех или иных состояний необходимо считаться; 3) допускается некоторый риск; 4) решение реализуется один или много раз |
Рассмотрим пример.
Пусть требуется провести осмотр машины с остановкой ее эксплуатации. Остановка машины приводит к снижению выпуска продукции. Отказ машины из-за необнаруженной вовремя неисправности вызывает ее остановку с потерей выпуска продукции, дополнительные затраты, связанные с устранением отказа.
Возможны три варианта решения:
Е1 - полный осмотр машины;
Е2 - минимальный осмотр;
Е3 - не проводить осмотр.
При этом машина может находиться в одном из трех состояний:
F1 - неисправностей нет;
F2 - имеется незначительная неисправность, которая могла бы быть устранена во время технологических пауз;
F3 - имеется серьезная неисправность.
Известно, что состояние F3 встречается вдвое чаще, чем любое другое состояние, т.е. вероятности появления состояний можно представить в виде вектора {q1 = q2 = 0.25; q3 = 0.5}.
Результатом вариантов являются затраты на осмотр, устранение неисправностей, потери в продукции от простоя и брака (таблица 8.3).
Как видно из таблицы 8.3 согласно ММ-критерию (позиция крайней осторожности), BL-критерию, G-критерию (позиция компромисса) лучшим решением с точки зрения затрат и отсутствия риска является проведение полного осмотра машины (вариант E1). S-критерий предписывает минимальную проверку (вариант E2), при этом максимально возможные потери в случае, если оптимальным являлся другой вариант, будут минимальны. HW-критерий (позиция средневзвешенного наилучшего и наихудшего результатов) предлагает отказаться от осмотра (вариант E3).
Таблица 8.3 - Варианты решения о проверках машины и их оценки согласно различным критериям
| Матрица решений | ММ-критерий | BL-критерий | ||||||
| F1 | F2 | F3 | 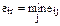
| max eir | 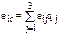
| max eir | ||
| E1 | -16 | -17 | -26 | -26 | -26 | -21.25 | -21.25 | |
| E2 | -12 | -20 | -31 | -31 | -23.5 | |||
| E3 | -24 | -41 | -41 | -26.5 |
| Матрица решений | S-критерий | HW-критерий | ||||||||
| F1 | F2 | F3 | aij | 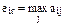
| max eir | 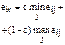
| max eir | |||
| F1 | F2 | F3 | ||||||||
| E1 | -16 | -17 | -26 | -21 | ||||||
| E2 | -12 | -20 | -31 | -21.5 | ||||||
| E3 | -24 | -41 | -20.5 | -20.5 |
| G-критерий | |||||
| eijqj | 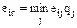
| max eir | |||
| F1 | F2 | F3 | |||
| E1 | -4 | -4.25 | -13 | -13 | -13 |
| E2 | -3 | -5 | -15.5 | -15.5 | |
| E3 | -6 | -20.5 | -20.5 |
Таким образом, большинство критериев склоняются к проведению полного осмотра машины. Однако, следует отметить, что выбор некоторых из них зависит от субъективной информации. Например, HW-критерий зависит от весового множителя c (было принято с=0.5), который выражает уровень риска (соотношение между оптимистической и пессимистической позициями). Если вероятности qj состояний машины известны не точно, то результаты, полученные по BL- и G-критериям, содержат некоторый риск. Число реализаций решения также оказывает влияние на окончательный выбор решения. Если решение реализуется один раз, то лучше придерживаться MM-критерия, риск при этом полностью исключается. Из сказанного следует, что для использования описанных критериев требуется по возможности полная информация о рассматриваемой ситуации, иначе принимаемые решения подвержены влиянию субъективизма ЛПР.
Дата добавления: 2016-02-02; просмотров: 2668;
