Розрахунки за правилом складних відсотків в умовах змін вихідних параметрів
За правилом складних відсотків вартісні характеристики фінансової угоди (кінцева та початкова вартість коштів) безпосередньо залежать від строку (кількості періодів) та норми дохідності фінансової операції.
Класична формула нарощення складних відсотків (3.1) передбачає, що протягом усіх періодів п ставка дохідності і є сталою величиною.
Однак в реальних економічних умовах, ринкові ставки дохідності весь час змінюються, отже, у довгострокових фінансових угодах фіксувати ставку нарощування (або дисконтування) на весь термін угоди на визначеному початковому рівні не завжди доцільно. У разі плаваючих (змінних) ставок дохідності, зазвичай весь строк угоди розбивають на періоди, протягом яких ставка є незмінною.
Таким чином, коли впродовж терміну угоди ставки дохідності змінюються в часі, але в певні терміни, то нарощену за складними відсотками суму визначають за формулою:
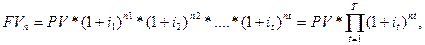(3.15)
де Т— загальна кількість періодів нарощення; і — ставка дохідності у періоді t;
п — тривалість t періоду, у якому ставка дохідності не змінюється.
Для визначення середньої ставки дохідності складних відсотків і за повний строк дії фінансової угоди N необхідно розв'язати відносно і таке рівняння:
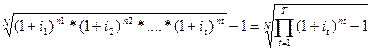(3.16)
Отже, множник нарощення за середньою ставкою складних процентів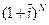 
визначають за формулою зваженої середньої геометричної величини.
Окрім ставки дохідності, іншим змінним вихідним параметром фінансової операції є загальна кількість періодів нарощеннячи дисконтування. У практиці фінансових розрахунків часто трапляються ситуації, коли за фіксованого загального строку угоди п змінюється кількість періодів нарахувань коштів. Наприклад, за банківським депозитом вказується річна ставка складних процентів і, а нарахування здійснюють щомісяця чи щокварталу тощо.
Отже, у деяких фінансових угодах капіталізація (нарахування) процентів відбувається m - разів однаковими частками через однакові проміжки часу протягом кожного періоду часу t.
В такому разі класична формула (3.1) для визначення майбутньої вартості за правилом складних відсотків, набуває вигляду:
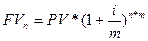(3.17)
т — кількість нарахувань відсотків протягом одного періоду часу.
Зазначимо, що коли т = 1 (тобто загальна кількість нарахувань процентів співпадає з загальною кількістю періодів), то вираз (3.17) повністю співпадає з виразом (3.1).
Приклад 3.Вкладник поклав на депозит до банку 1 тис. грн. під 16% річних. Умовами угоди передбачено, що на цю суму банк нараховує складні відсотки щокварталу. Знайти суму, що акумулюється на депозитному рахунку через рік.
За формулою (3.17) маємо:
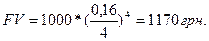
З використанням фінансових таблиць розрахунок набуває наступного вигляду:
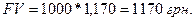
Таким чином, коли виплати здійснюють за правилом складних відсотків кілька разів на рік, то фактична річна дохідність фінансової угоди більша від задекларованої річної дохідності за рахунок реінвестування коштів.
Дата добавления: 2016-02-02; просмотров: 662;