Распространение ударных волн в скважине

При срабатывании в скважине, заполненной жидкостью, перфоратора, торпеды или порохового генератора давления (ПГД) может произойти полное поглощение ударной волны пластом даже в условиях заполнения скважины жидкостью до устья. Близкая к этой возникает ситуация при отстреле перфоратора в скважине со сниженным уровнем. В таких ситуациях возникают проблемы по установлению факта и полноты срабатывания перфоратора. Для перфораторов, спускаемых на трубах , единственный путь решения проблемы состоит в подъёме перфоратора на дневную поверхность. Если поглощение ударных волн пластом отсутствует, то независимо от того, инициируется срабатывание одного заряда или группы, по жидкости и по обсадной колонне распространяются ударные волны. За пределами интервала срабатывания перфоратора формируются только две волны. Одна из них распространяется в скважинной жидкости в сторону устья, другая - в сторону забоя.

Среди факторов, способных оказать влияние на распространение таких волн, нужно отметить дисперсию, упругость самих труб, а также диссипацию энергии . Таким образом, ослабление ударной волны до акустической должно произойти уже на расстоянии всего лишь нескольких десятков метров от интервала срабатывания взрывного устройства.

Однако, как показывает практический опыт, интенсивные возмущения от срабатывания перфоратора или порохового генератора давления могут распространяться в жидкостях, заполняющих обсаженные скважины, без значительного затухания на многие километры. Хорошо известны случаи достижения возмущениями устья скважины с выбросом ограниченного объёма жидкости при проведении перфорации на глубине пяти и более километров. Не получили также должного объяснения случаи выброса из скважины десятков метров кабеля при срабатывании порохового генератора давления. И это несмотря на то , что пороховые заряды спускали в скважину заполненную жидкостью на кабеле с постоянным контролем и воспламеняли их только после достижения зарядами заданной глубины ( как правило нескольких километров). Не редки случаи забрасывания кабельного наконечника в зазор между НКТ и обсадной колонной при срабатывании полностью разрушающегося перфоратора, спущенного на кабеле через НКТ, в условиях малых расстояний от интервала перфорации до башмака НКТ. Всё это говорит о том, что в скважинах заполненных жидкостью могут формироваться особые волны, способные не только распространяться на большие расстояния, но и перемещать находящиеся в жидкости предметы, которые обычные волны ( в том числе и ударные) должны огибать. Для объяснения наблюдаемых эффектов целесообразно обратиться к теории солитонов, то есть уединённых волн, распространяющихся по поверхности океана без затухания на десятки и сотни километров.

Многие исследователи предполагают, что в уединённой волне происходит одновременное движение частиц жидкости в продольном и поперечном направлениях. Поэтому уединённые волны не являются ни продольными, ни поперечными, а представляют собой симбиоз тех и других. Одна из главных проблем распространения уединённых волн состоит в разработке основ теории сохранения ими амплитуды. Попытка объяснить отсутствие затухания амплитуды волны компенсацией дисперсии нелинейностью, связанной с зависимостью амплитуды волны от скорости её распространения, является не вполне состоятельной. Тем более, что нужно компенсировать ещё и диссипацию энергии.

Одновременное движение частиц жидкости в продольном и поперечном направлениях в уединённой волне определяет и особенность действия её на стенку трубы (НКТ или обсадной). Со специфическим движением частиц жидкости в волне связано и появление сжимающего давления, направленного к оси трубы.

Рассмотрим подробнее причины радиального сжатия жидкости в пределах волны, распространяющейся в цилиндрической трубе. Прежде всего представим волну как совокупность отдельных волн с возрастающей величиной давления от волны к волне в направлении к общему фронту. Таким образом уединённая волна в трубе напоминает модулированную радиоволну. В пределах каждой отдельной волны, входящей в состав совокупной, частицы жидкости движутся в продольном и поперечном направлении, что в итоге приводит к круговым перемещениям их. Сложение скоростей частиц жидкости вдоль оси трубы формирует “ стержень “ в котором жидкость движется с огромными скоростями. Давление в жидкости вокруг “ стержня “ в пределах волны может быть ниже даже гидростатического в скважине, несмотря на очень высокое давление на фронте волны.

Представленный качественный анализ указывает на принципиальную возможность распространения в трубах, заполненных жидкостью, интенсивных возмущений с очень малым затуханием на расстояние многих километров. Однако, в случае отсутствия в стенке труб сквозных дефектов виде отверстий или трещин, такая волна не представляет опасности для конструкции скважины. В то же время на сквозных дефектах труб будет происходить локальное выделения огромной энергии волны с развитием дефектов и воздействием через них на затрубное пространство.

Выход акустической волны на границу раздела жидкость – воздух.

Прежде всего рассмотрим в каких случаях возможно перемещение предметов, находящихся в жидкости под действием ударной или акустической волны. Если предмет находится на пути распространения подводной ударной волны на значительном расстоянии от границы жидкость – воздух, то при малом сечении предмета его перемещение будет незначительным. Иначе обстоит дело в случае нахождения того же предмета вблизи границы раздела жидкость – газ . При достижении ударной волной границы жидкость – газ, в газ выйдет преломлённая волна сжатия , а по жидкости будет распространяться волна разрежения. Когда волна разрежения создаст в жидкости на глубине h напряжение растяжения , превышающее сумму гидростатического давления на этой глубине и динамической прочности жидкости на разрыв, произойдёт кавитационный разрыв сплошности жидкости. Если граница жидкость – воздух находится на уровне верхнего фланца устьевой арматуры или открытой перфораторной задвижки , то кавитационный разрыв сплошности будет сопровождаться выбросом части оторванного слоя жидкости из скважины. В случае нахождения предмета в оторванном слое и отсутствия якорящих устройств предмет может быть увлечён жидкостью и выброшен из скважины.

За первым разрывом сплошности жидкости последуют другие разрывы и процесс продолжится до тех пор, пока в скважинной жидкости будут возникать достаточные растягивающие напряжения, которые зависят от формы волны. Роль свободной поверхности, на которой происходит скачёк акустического сопротивления, при втором и последующих разрывах будут играть предыдущие кавитационные разрывы. Понятно, что давление на границе кавитационного разрыва близко к нулю. Менее определённой является динамическая прочность жидкости на разрыв. По экспериментальным данным Бриджа вода, свободная от механических примесей и газовых включений, выдерживает давление на разрыв в десятки МПа. Поскольку разрывы в скважинной жидкости не достигают глубины в сотни метров гидростатическим давлением на уровне кавитационного разрыва можно пренебречь и учитывать только прочность жидкости на разрыв.

Для получения принципиальных соотношений рассмотрим упрощённую задачу. Пусть на поверхность раздела падает плоская волна экспоненциального профиля:

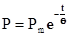, (4.6)

где 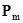- давление на фронте волны; t –текущее время, отсчитанное от фронта волны; 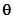- показатель падения давления в волне.

Применив метод зеркального отображения источника и стока, найдём результирующее давление на глубине 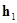(см Рис. 4.19)

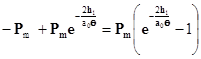(4.7),

где а₀ – скорость звука в скважинной жидкости.

Приравнивая результирующее давление из 9.19 прочности жидкости на разрыв - 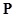_к получим

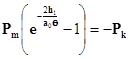
(4.8)

Из (9.20) получим выражение для толщины первого выброшенного слоя жидкости:

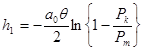(9.21)

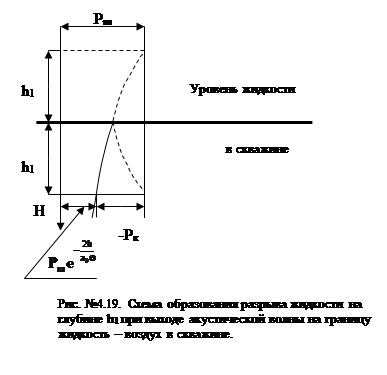Из представленной зависимости следует, что глубина разрыва сплошности жидкости h₁ в скважине зависит не от абсолютного значения давления на фронте волны Р_m , но определяется относительной прочностью воды на разрыв. Чем ближе значения Р_m и P_К , тем на большей глубине будет происходить образование кавитационнной полости. Значительное влияние на глубину разрыва h₁ оказывает показатель падения давления в волне 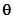. В свою очередь показатель 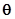зависит от количества и общей массы одновременно срабатывающих в скважине кумулятивных зарядов.

Рассмотрим движение первого оторванного слоя . В нулевом приближении (пренебрегая сопротивлением воздуха) движение этого слоя тормозится силой тяжести.

Поэтому дифференциальное уравнение движения запишется в следующем виде.

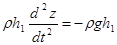, (4.10)

где 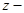вертикальная координата, 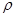- плотность воды.

При достаточно большой общей массе зарядов и отсутствии газовых включений в скважинной жидкости величина h₁ может составлять сотни метров. Движение столба скважинной жидкости выше зоны разрыва вверх и даже частичный выброс её из скважины приведёт к возникновению временной депрессии на пласт и поступлению из последнего пластового флюида в скважину. Для газовых скважин или нефтяных, эксплуатирующих пласты с большим газовым фактором, это может привести к поступлению в скважину газа и несанкционированному фонтанированию.