ЗАВИСИМОСТЬ ПЛОТНОСТИ ВОЗДУХА ОТ ЕГО ТЕМПЕРАТУРЫ И
ДАВЛЕНИЯ
При изменении давления и температуры изменяется плотность воздуха.
Согласно закону Бойля-Мариотта плотность воздуха будет тем больше, чем больше давление, а согласно закону Гей-Люссака плотность воздуха тем больше, чем меньше температура воздуха. Объединив эти два закона для определения зависимости между плотностью, давлением и температурой воздуха, получим уравнение состояния газа (закон Бойля-Мариотта - Гей-Люссака).
Таким образом, можно сделать заключение, что чем выше давление и ниже температура, тем больше плотность воздуха. Поэтому наибольшая плотность воздуха зимой в морозную погоду, а наименьшая летом в теплую погоду. Также следует заметить, что плотность влажного воздуха меньше, чем сухого (при одних и тех же условиях). Поэтому иногда учитывают и влажность, вводя при этом в расчеты соответствующие изменения.
С высотой плотность воздуха падает, так как давление в большей степени падает, чем понижается температура воздуха.
ФИЗИЧЕСКИЕ СВОЙСТВА ВОЗДУХА
На характер обтекания самолета воздушным потоком и на величину сил, возникающих при взаимодействии частей самолета и воздушного потока, существенное влияние оказывают физические свойства воздуха: инертность, вязкость, сжимаемость.
Инертность - свойство воздуха сопротивляться изменению состояния покоя или равномерного прямолинейного движения (второй закон Ньютона). Мерой инертности является массовая плотность воздуха. Чем больше массовая плотность воздуха, тем большую силу необходимо приложить к воздуху, чтобы вывести его из состояния покоя или равномерного прямолинейного движения. Следовательно, чем больше сила самолета, действующего на воздух, тем больше сила, действующая со стороны воздуха на самолет (третий закон Ньютона).
Вязкость-свойство воздуха сопротивляться взаимному сдвигу частиц. Молекулы воздуха обладают определенной скоростью беспорядочного хаотического движения, зависящего от температуры, а также скоростью общего поступательного движения. Попадая из быстро движущегося слоя в медленный, молекулы ускоряют движение медленно движущихся молекул, и наоборот - медленно движущиеся молекулы, попадая в быстро движущийся слой воздуха, притормаживают быстро движущиеся молекулы.
При движении самолета в воздушном потоке возникает сопротивление трения, которое определяет вязкость воздуха. Вязкость воздуха также определяет динамический коэффициент вязкости. Чем больше температура воздуха, тем больше коэффициент вязкости, обусловленный увеличением хаотического движения молекул и ростом эффективности воздействия одного слоя воздуха на другой.
Сжимаемость - свойство воздуха изменять свою плотность при изменении давления.
МЕЖДУНАРОДНАЯ СТАНДАРТНАЯ АТМОСФЕРА
Изменение основных параметров воздуха (давления, температуры и плотности) влияет на величину сил, возникающих при движении самолета в воздушном потоке. Поэтому при полетах в разных метеорологических и климатических условиях изменяются летные и аэродинамические характеристики самолетов.
Чтобы охарактеризовать летные и аэродинамические данные самолетов при одинаковых параметрах воздуха, всеми странами принята единая Международная стандартная атмосфера (МСА).
Таблица МСА составлена на основании среднегодовых условий средних широт (широта около 45°) на уровне моря при влажности нуль процентов и следующих параметрах воздуха:
барометрическое давление В =760 мм рт. ст. (Ро= 10330 кгс/м2);
температура t=+15°C (То=288 К);
массовая плотность 0,125 кгс см4;
удельный вес 1,225 кгс/см3.
Согласно МСА температура воздуха в тропосфере падает на 6,5°С на каждые 1000 м.
Таблица МСА
| |
| Высота H, м | Давление на высоте P H мм | Температура на высоте t H в градусах С | Плотность воздуха r |
| 760,0 | 15,0 | 1,2255 | |
| 751,0 | 14,4 | 1,2137 | |
| 742,1 | 13,7 | 1,2021 | |
| 733,3 | 13,1 | 1,1906 | |
| 724,6 | 12,4 | 1,1791 | |
| 716,0 | 11,8 | 1,1677 | |
| 707,4 | 11,1 | 1,1564 | |
| 699,0 | 10,5 | 1,1452 | |
| 690,6 | 9,8 | 1,1340 | |
| 682,2 | 9,2 | 1,1230 | |
| 674,0 | 8,5 | 1,1120 | |
| 634,1 | 5,3 | 1,0581 | |
| 596,1 | 2,0 | 1,0067 | |
| 560,0 | -1,2 | 0,9578 | |
| 525,7 | -4,5 | 0,9093 | |
| 493,1 | -7,7 | 0,8633 | |
| 462,2 | -11,0 | 0,8192 | |
| 432,8 | -14,2 | 0,7768 | |
| 404,8 | -17,5 | 0,7361 | |
| 378,5 | -20,7 | 0,6971 | |
| 353,7 | -24,0 | 0,6596 | |
| 330,1 | -27,2 | 0,6238 | |
| 307,8 | -30,5 | 0,5894 | |
| 286,7 | -33,7 | 0,5565 | |
| 266,8 | -37,0 | 0,5250 | |
| 248,0 | -40,2 | 0,4949 | |
| 230,4 | -43,5 | 0,4662 | |
| 213,7 | -46,7 | 0,4387 | |
| 198,1 | -50,0 | 0,4125 | |
| 90,2 | -56,0 | 0,1935 | |
| 40,9 | -56,5 | 0,0880 |

АЭРОДИНАМИКА
Аэродинамика это наука о законах движения воздушной (газовой) среды и силового взаимодействия этой среды с граничными поверхностями.
Граничные поверхности разделяются на:
- внешние – поверхности тел, обтекаемые потоком;
- внутренние – газ движется внутри различных каналов.
При малых скоростях полета воздух принимается как несжимаемая среда. Но с ростом скорости полета (на трасзвуковых и сверхзвуковых скоростях) необходимо учитывать свойство сжимаемости среды. При полетах на небольших высотах воздушную среду принимают сплошной. Но при полете на больших высотах, где плотность воздуха очень мала, необходимо уже применять другие зависимости, которые должны учитывать несплошность среды. На высотах до 15 км (высоты полета гражданских самолетов) во всех случаях принимаем среду сплошной. Это справедливо, ведь размеры исследуемых тел (самолет, вертолет, планер и другие летательные аппараты) гораздо больше свободного пробега молекул.
Основные параметры среды
- g = 9,81 – ускорение свободного падения (м/с 2 );
- V m ρ = (плотность) – это масса газа (жидкости) заключенная в единице объема (кг/м 3 ), для воздуха ρ=1,225;
- γ = ρ ⋅ g (удельный вес) - это вес газа (жидкости) заключенная в единице объема (Н/м 3 );
- массовые силы – силы, действующие на каждый элемент среды (сила тяжести, сила инерции);
- поверхностные силы – силы, действующие на поверхности S со стороны окружающей среды (трение, давление);
- силы трения – силы, действующие по касательной к поверхности (Н/м 2 );
- силы давления – силы, действующие перпендикулярно поверхности (Н/м 2 ).
Основные свойства среды
- Вязкость – способность сопротивляться деформации сдвига. Идеальная среда – среда, в которой отсутствуют вязкость.
- Сжимаемость – способность среды изменять свой объем (плотность) при изменений давления и температуры: R T p = ⋅ ρ ; где R – газовая постоянная (для воздуха R=29,27); Т – температура (град К); T=t+273; t – температура (град С).
- Скорость звука – скорость распространения звука в газовой среде:6 k R T 20 1, T p k d dp a = = ⋅ = ⋅ ⋅ = ⋅ ρ ρ; где k=1.4.
Процессы изменения состояния газа
- Изотермический – при изменении состояния газа температура постоянна (dT=0).
- Изобарный – при изменении состояния газа давление постоянно (dР=0).
- Изохорный– при изменении состояния газа объем постоянный (dV=0).
- Изотропный – при изменении состояния газа энергия среды постоянна (dЕ=0).
- Адиабатический – при изменении состояния газа отсутствует теплообмен.
- Изоэнтропический – при изменении состояния газа энтропия (Энтропия — это сокращение доступной энергии вещества в результате передачи энергии) остается постоянной (dS=0).
Течение газа или жидкости выражается двумя важными уравнениями: уравнением неразрывности потока и уравнением Бернулли.
Уравнение неразрывности потока отражает закон сохранения массы: количество входящего потока равно количеству выходящему. Например, на рис. 1 расходы во входном и выходном сечениях равны:
q1 = q2.
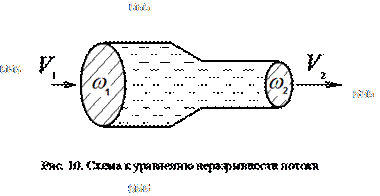
Рисунок 1. Схема к уравнению непрерывности потока
С учётом, что q = V ω, получим уравнение неразрывности потока:
V1 ω1 = V2 ω2 .
Если отсюда выразим скорость для выходного сечения
V2= V1 ω1 / ω2 ,
то легко заметить, что она увеличивается обратно пропорционально площади живого сечения потока. Такая обратная зависимость между скоростью и площадью является важным следствием уравнения неразрывности и применяется в технике, например, при тушении пожара для получения сильной и дальнобойной струи воды.
Рассмотрим пример.
Как изменится скорость потока, если диаметр напорной трубы d уменьшится в два раза? Площадь живого сечения такой трубы
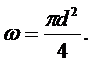
Тогда отношение площадей в формуле (18) будет равно 4.
Таким образом, при уменьшении диаметра трубы в два раза — скорость потока увеличится в четыре раза. Аналогично, если диаметр уменьшится в три раза — скорость возрастёт в девять раз.
Уравнение Бернулли
Рассмотрим поток газа, проходящий по трубопроводу переменного сечения. В первом сечении приведённое полное давление равно Рпр.п1. При прохождении по трубе часть Рпр.п1 необратимо потеряется из-за проявления сил внутреннего трения газа и во втором сечении энергетическая характеристика уменьшится до Рпр.п2 на величину потерь давления D Рпот.
Уравнение Бeрнýлли для газа в простейшем виде записывается так:
Рпр.п1 = Рпр.п2+ DРпот .
Уравнение Бeрнýлли в традиционной записи получим, если в последнем равенстве раскроем значения приведённых полных давлений Рпр.п1 и Рпр.п2 по:
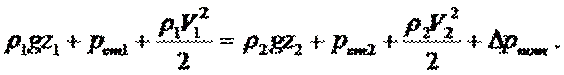
Энергетический смысл уравнения Бeрнýлли для газа заключается в том, что оно отражает закон сохранения энергии, а геометрический не рассматривается, так как величины в нём выражаются в единицах давления (Па), а не напора (м).

Разность давлений и потери давления
Движение газа происходит только при наличии разности приведённых полных давлений DРпр = Рпр.п1 – Рпр.п2 от бóльшего давления Рпр.п1 к меньшему Рпр.п2. Например, так работает естественная вентиляция для удаления воздуха из помещений зданий.
Потери давления DРпот отражают потерю полной энергии потока при движении газа. Например, чем длиннее воздуховод, меньше его проходное сечение, шероховатее его стенки, тем больше будут потери давления DРпот в системе вентиляции, что может ухудшить удаление несвежего воздуха из помещений.
При установившемся движении газа разность давлений численно равна потерям давления: DРпр = DРпот .
Таким образом, «разность давлений» является причиной движения газа, а «потери давления» — следствием. Измеряются они в одних и тех же единицах СИ — паскалях (Па).
ЧИСЛО МАХА, отношение скорости тела или (газа или жидкости) к скорости звука вокружающей среде. Таким образом, число Маха, равное 1, выражает локальную скорость звука. Самолет,летящий со скоростью ниже 1 Маха , считается дозвуковым, т.е. летящим со скоростью меньше скоростизвука. СВЕРХЗВУКОВОЙ ПОЛЕТ означает полет со скоростью выше 1 Маха. Числа Маха названы в честьЭрнста МАХА, который исследовал сверхзвуковые скорости и ударные волны.
Дата добавления: 2016-02-02; просмотров: 22527;
