Взаємодія антиген-антитіло. Методи її вивчення.
Нагадаю, головною функцією антитіл (АТ) є специфічне зв'язування антигену (АГ). В основі реакції антиген-антитіло лежить взаємодія між епітопами АГ та активними центрами АТ, яка ґрунтується на принципі комплементарності. Антитіла розпізнають не окремі хімічні групи у складі епітопу, а просторову форму епітопів, розрізняючи при цьому не тільки відмінності в розподілі зарядів, оптичну і стереоізомерію, а також мінімальні відмінності в амінокислотній послідовності. Внаслідок такої тонкої специфічності більшість антитіл здатна зв’язуватися тільки із нативними антигенами, які зберігають третинну структуру, необхідну для множинних взаємодій між епітопом та активним центром.
При контакті специфічних антитіл з антигеном між амінокислотними залишками антигензв’язуючого центру АТ та епітопами АГ виникають численні нековалентні зв’язки, зокрема:
1. Електростатичні іонні, які виникають між двома протилежно зарядженими іонізованими групами, найчастіше карбоксильними і аміногрупами білків. Також є електростатичні полярні, пов’язані з утворенням диполей.
2. Водневі зв’язки, які утворюються між гідрофільними групами.
3. Сили Ван дер Ваальса, які виникають в результаті взаємодій поверхневих електронних хмар контактуючих ділянок молекул.
4.Неполярні гідрофобні взаємодії, утворення яких обумовлене енергетичною перевагою контакту гідрофобних ділянок молекул між собою у порівнянні із їх взаємодією з водою. Саме гідрофобні зв’язки забезпечують до 50% усієї спорідненості між антигенами і антитілами. Рис 9.2.
Порівняно із ковалентними зв’язками сили нековалентних взаємодій нарізно досить слабкі, проте при великій кількості слабких взаємодій сумарна енергія зв’язування виходить досить значною. Сила нековалентного зв’язку залежить, перш за все, від відстані між взаємодіючими хімічними групами. Наприклад, при електростатичних взаємодіях вона обернено пропорційна квадрату відстані між групами, а при вандерваальсових - обернено пропорційна відстані між ними в сьомому ступені.

Для зв’язування епітопу із активним центром антитіла (паратопом) необхідне одночасне утворення декількох нековалентних зв’язків. При певному рівні комплементарності величина енергії притягання стає достатньою, щоб не відбувалося термодинамічного розриву зв’язків.
Разом з тим, при перекриванні електронних оболонок молекул АТ і АГ між ними виникають і сили відштовхування, величина яких обернено пропорційна 12-ому ступеню величини міжмолекулярної відстані. Саме співвідношення між силами притягання та відштовхування обумовлює взаємодію АГ з АТ (рис.9.5).
З кількісної сторони специфічність взаємодії АГ-АТ характеризується через афінність антитіл. Афінністю або спорідненістю антитілдо антигену називають результуючу силу їх взаємодій, яка є сумою перерахованих вище сил притягання та відштовхування, що діють між активним центром АТ і епітопом АГ. Термін «афінність» стосується взаємодії лише одного центру зв’язування антитіла з моновалентним антигеном, точніше з одним епітопом. Афінність відображає здатність антитіл формувати стабільні імунні комплекси (АГАТ).
В найпростішому випадку взаємодія АГ з АТ може бути описана кінетичною формулою хімічної реакції першого порядку:
АГ + АТ 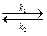 АГАТ, де
АГАТ, де
АГ – вільний антиген;
АТ – вільне антитіло;
АГАТ– комплекс антиген-антитіло;
κ1- константа швидкості асоціації;
κ2- константа швидкості дисоціації комплексу антиген-антитіло (АГАТ).
Оскільки нековалентні зв’язки між епітопом і активним центром здатні дисоціювати, утворення імунних комплексів – процес оборотний і, застосувавши закон діючих мас, можна розрахувати константу рівноваги або афінності κа, яка власне і характеризує ефективність утворення комплексу.
υ1 = k1 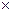 [АГ]
[АГ] 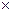 [АТ]
[АТ]
υ2 = k2 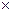 [АГАТ]
[АГАТ]
За умов рівноваги, коли V1=V2 можна записати:
k1 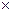 [АГ]
[АГ] 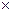 [АТ] = k2
[АТ] = k2 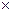 [АГАТ],
[АГАТ],
звідки
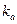 =
= 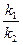 =
= 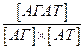 ,М-1 або л/моль
,М-1 або л/моль
Константа афінності κа виражається у зворотних молях – л/моль, що на перший погляд може здатися дивним. Таке позначення повязано з тим, що величину 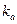 отримують приділенні однієї концентрації (моль/л) на добуток двох інших концентрацій:
отримують приділенні однієї концентрації (моль/л) на добуток двох інших концентрацій:
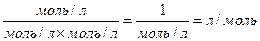
Про специфічне зв'язування говорять тоді, коли κа перевищує 105 М-1, тобто коли швидкість утворення комплексу перевищує швидкість його розпаду на 5 порядків. Для високоафінних або високоспецифічних антитіл κа > 108 М-1. Найменшою ефективністю взаємодії характеризуються антитіла проти вуглеводів κа <106 М-1.

На практиці часто використовують константу дисоціації комплексу АГ-АТ kd, яка зв’язана із κапростим співвідношенням:
kd = 1/κа
Очевидно, чим меншою буде kd або навпаки, більшою κа , тим міцнішим буде комплекс АГ-АТ.
Реакція АГ-АТ є екзотермічною, тобто протікає із вивільненням енергії, надлишок якої може витрачатися на конформаційні зміни переважно у третинній структурі АГ чи АТ, які необхідні для досягнення оптимальної комплементарності. Такі зміни конформації можуть бути потрібними або для того, щоб забезпечити сам контакт між АГ та АТ, або для того, щоб вивести із зони контакту ті амінокислотні залишки, які б створювали сили відштовхування, якби залишилися б у попередньому стані.
Константа афінності - κає термодинамічним параметром, який характеризує зміну вільної енергії взаємодії АГ-АТ ∆F і її можна розрахувати за формулою:
∆F = - RT ln κа, де
R – газова постійна;
T- абсолютна температура (Кельвін).
Термодинамічнo ka визначається різницею вільної енергії ∆ F між станами антигену і антитіл, коли вони не взаємодіють, і після утворення комплексу. Для реакції антиген-антитіло ∆F = -31.5 – -43.2 кДж/моль (порівняно із
-229,53 кДж/моль для утворення двох ковалентних зв'язків Н-O у молекулі води), тобто реакція іде із зменшенням вільної енергії,і є енергетичне вигідною. Надлишок енергії використовується на необхідні конформаційні зміни в антигені та антитілі для досягнення оптимальної комплементарності. Зважаючи на те, що як антигенні детермінанти антигену, так і активні центри антитіл мають підвищену атомну мобільність, стає зрозумілим, що вони взаємно конформують один одного.
Загальна зміна вільної енергії при комплексоутворенні складається з двох термодинамічних величин - зміни ентальпії і ентропії:
∆F = ∆Н - T∆S
Визначення ∆Н можна провести експериментально за допомогою простих калориметричних вимірів.
Константа афінності є важливою характеристикою антитіл, тому її треба вміти розраховувати. Так, для взаємодії однієї субпопуляції антитіл з моно- валентним антигеном (наприклад, гаптен зв’язується з Fab –фрагментом антитіл) проводяться такі розрахунки:
 Згідно з АГ + АТ
Згідно з АГ + АТ 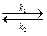 АГАТ (1)
АГАТ (1) 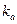 =
= 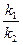 =
= 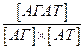 (2)та системоюрівнянь
(2)та системоюрівнянь
[АТ]з=[АТ] +[ АГ·АТ ]
[АГ]з=[АГ] +[ АГ·АТ ] (3),
де [АТ]з і [АГ]з- загальна концентрація АТ і АГ,
[ АГ·АТ ] - концентрація зв’язаних АТ чи АГ, [АТ] і [АГ]- концентрація вільних АТ чи АГ.
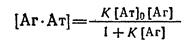 В результаті перетворень одержуємо (4):
В результаті перетворень одержуємо (4):
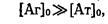 Одним із часто використовуваних способів розрахунку константи є дослідження залежності вмісту комплексу, що утворюється, від загальної концентрації антигену [АТ]з. За умови досить високих концентрацій антигену в системі виконується -
Одним із часто використовуваних способів розрахунку константи є дослідження залежності вмісту комплексу, що утворюється, від загальної концентрації антигену [АТ]з. За умови досить високих концентрацій антигену в системі виконується -
 Тоді рівняння (4)стає таким: (5) рос.мова
Тоді рівняння (4)стає таким: (5) рос.мова
[ АГ·АТ ] =
ка [АТ]з· [АГ]з / 1+ ка [АГ]з
Ця залежність є аналогом рівняння Міхаеліса –Ментен в ферментативній кінетиці. З рівняння (5) випливає, що при високих (предельных) значеннях [АГ]з ([АГ]з >> [АТ]з), концентрація комплексу [АГ·АТ] спрямована до загальної концентрації центрів [АТ]з, оскільки, поділивши чисельник і знаменник у рівнянні 5 на [АГ]з та знехтувавши 1/[АГ]з як дуже малою величиною, отримаємо [АГ·АТ] = [АТ]з (графік).
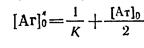 При розрахунку
При розрахунку 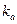 визначаютьконцентрацію антигену[АГ]'з, при якій половина антитіл знаходиться у вигляді комплексу з антигеном [АГ·АТ] = [АТ]з/2. Враховуючи (3) і (4), отримуємо (6):
визначаютьконцентрацію антигену[АГ]'з, при якій половина антитіл знаходиться у вигляді комплексу з антигеном [АГ·АТ] = [АТ]з/2. Враховуючи (3) і (4), отримуємо (6):
[АГ]з'=1/ Ка +[АТ]з/2 або рос. мовою:
 |
 Для розуміння методологічних підходів розглянутих методів звернемося до їх ілюстративного схематичного зображення:
Для розуміння методологічних підходів розглянутих методів звернемося до їх ілюстративного схематичного зображення:
Для аналіза комплексоутворення розроблено декілька математичних підходів, декілька рівнянь, найбільш вживаним є метод Скетчарда, заснований на дослідженні залежності співвідношення рівноважної концентрації комплекса [АГ·АТ] /[АГ] від концентрації комплекса [АГ·АТ]. Для спрощення можна оперувати такими поняттями як:
[B] (bound)- концентрація зв'язаного антигену, [ АГ·АТ ] (3)
[F] (freе) - концентрація вільного антигену; [АГ] (3)
п — кількість центрів зв'язування антитіл (ціле антитіло має два центри зв'язування, а Fab- фрагмент - один).
 Рівняння Скетчарда: [АГ·АТ] /[АГ]=
Рівняння Скетчарда: [АГ·АТ] /[АГ]=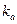 ·[АТ]з -
·[АТ]з - 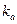 ·[АГ·АТ]=
·[АГ·АТ]=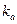 ([АТ]з-[АГ·АТ]) згідно з
([АТ]з-[АГ·АТ]) згідно з 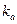 =
= 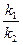 =
= 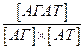 та
та
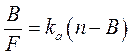 З скороченнями:
З скороченнями:
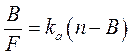
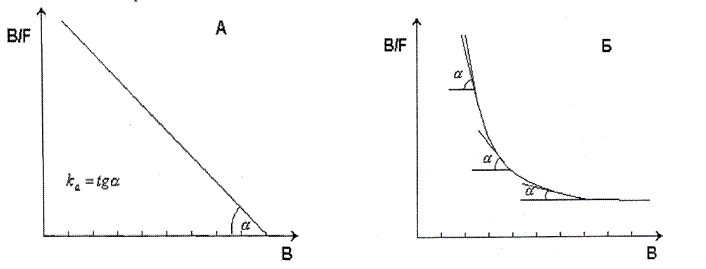
Рис. Графік Скетчарда для гомогенних (моноклональних, А) і
Дата добавления: 2016-02-02; просмотров: 3369;
