Моделирование аналоговых устройств на функционально-логическом уровне.

На функционально-логическом уровне исследуют устройства, в качестве элементов которых принимают достаточно сложные узлы и блоки, считавшиеся системами на макроуровне. Поэтому необходимо упростить представление моделей этих узлов и блоков по сравнению с их представлением на макроуровне. Другими словами, вместо полных моделей узлов и блоков нужно использовать их макромодели.

Вместо двух типов фазовых переменных в моделях функционально-логического уровня фигурируют переменные одного типа, называемые сигналами. Физический смысл сигнала, т.е. его отнесение к фазовым переменным типа потока или типа потенциала, конкретизируют в каждом случае исходя из особенностей задачи.

Основой моделирования аналоговых устройств на функционально-логическом уровне является использование аппарата передаточных функций. При этом модель каждого элемента представляют в виде уравнения вход-выход, т.е. в виде:

Vвых = f(Vвх), (4.6)

где Vвых и Vвх— сигналы на выходе и входе узла соответственно. Если узел имеет более чем один вход и один выход, то скаляры Vвых и Vвх становятся векторами.

Однако известно, что представление модели в виде (4.6) возможно только, если узел является безынерционным, т.е. в полной модели узла не фигурируют производные. Следовательно, для получения (4.6) в общем случае требуется предварительная алгебраизация полной модели. Такую алгебраизацию выполняют с помощью интегральных преобразований, например, с помощью преобразования Лапласа, переходя из временной области в пространство комплексной переменной р. Тогда в моделях типа (4.6) имеют место не оригиналы, а изображения сигналов Vвых(р) и Vвх(р), сами же модели реальных блоков стараются по возможности максимально упростить и представить их моделями типовых блоков (звеньев) из числа заранее разработанных библиотечных моделей. Обычно модели

звеньев имеют вид:

Vвых(р) = h(p)Vвх(р),

где h(p) — передаточная функция звена.

В случае применения преобразования Лапласа появляются ограничения на использование нелинейных моделей, а именно: в моделях не должно быть нелинейных инерционных элементов.

Другое упрощающее допущение при моделировании на функционально-логическом уровне – не учитывается влияния нагрузки на характеристики блоков.

Собственно получение ММС из ММЭ оказывается вследствие принятых допущений значительно проще, чем на макроуровне: ММС есть совокупность ММЭ, в которых отождествлены сигналы на соединенных входах и выходах элементов. Эта ММС представляет собой систему алгебраических уравнений.

Таким образом, анализ аналоговых устройств сводится к следующим операциям:

1. заданную схему устройства представляют совокупностью звеньев и, если схема не полностью покрывается типовыми звеньями, то разрабатывают оригинальные модели;

2. формируют ММС из моделей звеньев;

3. применяют прямое преобразование Лапласа к входным сигналам;

4. решают систему уравнений ММС и находят изображения выходных сигналов;

5. с помощью обратного преобразования Лапласа возвращаются во временную область из области комплексной переменной р.

Для системы, состоящей из блоков с различными передаточными функциями изобразить ее ММС.

Пусть задана следующая схема:

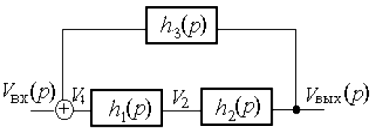
Рис 4.3 Модель устройства из трех блоков.

Тогда ММС данной схемы, характеризующаяся ее передаточной характеристикой, будет иметь вид:

V2 = h1(p)V1;

Vвых(p) = h2(p)V2;

V1 = Vвх(p) + h3(p)Vвых(p)

или

Vвых(p) =H(p)Vвх(p),

где H(p) = h1(p) h2(p) / (1 - h1(p) h2(p) h3(p))