Оптические дальномеры

В дальномерах измеряется не сама длина линии, а некоторая другая величина, относительно которой длина линии является функцией.

В геодезии применяют 3 вида дальномеров:

оптические (дальномеры геометрического типа),

электрооптические (светодальномеры),

радиотехнические (радиодальномеры).

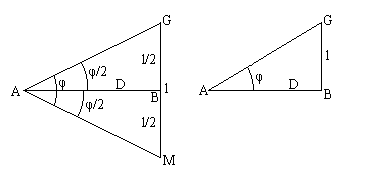
Рис.4.24

Геометрическая схема оптических дальномеров. Пусть требуется найти расстояние АВ. Поместим в точку А оптический дальномер, а в точку В перпендикулярно линии АВ - рейку.

Обозначим: l - отрезок рейки GM,
φ - угол, под которым этот отрезок виден из точки А.

Из треугольника АGВ имеем:

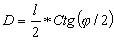(4.31)

или

D = l * Ctg(φ). (4.32)

Обычно угол φ небольшой (до 1o) , и, применяя разложение функции Ctgφ в ряд, можно привести формулу (4.31) к виду (4.32). В правой части этих формул два аргумента, относительно которых расстояние D является функцией. Если один из аргументов имеет постоянное значение, то для нахождения расстояния D достаточно измерить только одну величину. В зависимости от того, какая величина - φ или l, - принята постоянной, различают дальномеры с постоянным углом и дальномеры с постоянным базисом.

В дальномере с постоянным углом измеряют отрезок l, а угол φ - постоянный; он называется диастимометрическим углом.

В дальномерах с постоянным базисом измеряют угол φ, который называется параллактическим углом; отрезок l имеет постоянную известную длину и называется базисом.

Нитяной дальномер с постоянным углом. В сетке нитей зрительных труб, как правило, имеются две дополнительные горизонтальные нити, расположенные по обе стороны от центра сетки нитей на равных расстояниях от него; это - дальномерные нити (рис.4.25).

Нарисуем ход лучей, проходящих через дальномерные нити в трубе Кеплера с внешней фокусировкой. Прибор установлен над точкой А; в точке В находится рейка, установленная перпендикулярно визирной линии трубы. Требуется найти расстояние между точками А и В.

Рис.4.25

Построим ход лучей из точек m и g дальномерных нитей. Лучи из точек m и g, идущие параллельно оптической оси, после преломления на линзе объектива пересекут эту ось в точке переднего фокуса F и попадут в точки М и G рейки. Расстояние от точки A до точки B будет равно:

D = l/2 * Ctg(φ/2) + fоб + d, (4.33)

где d - расстояние от центра объектива до оси вращения теодолита;
fоб-фокусное расстояние объектива;
l - длина отрезка MG на рейке.

Обозначим (fоб + d) через c, а величину 1/2*Ctg φ/2 - через С, тогда

D = C * l + c. (4.34)

Постоянная С называется коэффицентом дальномера. Из Dm'OF имеем:

Ctg φ/2 = ОF/m'O; m'O= p/2; Ctg φ/2 = (fоб*2)/p,

где p - расстояние между дальномерными нитями. Далее пишем:

С = fоб/p. (4.35)

Коэффициент дальномера равен отношению фокусного расстояния объектива к расстоянию между дальномерными нитями. Обычно коэффицент С принимают равным 100, тогда Ctg φ/2 = 200 и φ = 34.38'. При С = 100 и fоб = 200 мм расстояние между нитями равно 2 мм .

Измерение нитяным дальномером наклонного расстояния. Пусть визирная линия трубы JK при измерении расстояния АВ имеет угол наклона ν, и по рейке измерен отрезок l (рис.4.26). Если бы рейка была установлена перпендикулярно визирной линии трубы, то наклонное расстояние было бы равно:

D = l0 * C + c.

Но l0 = l*Cos ν, поэтому

D = C*l*Cosν + c. (4.36)

Горизонтальное проложение линии S определим из Δ JKE :

S = D*Cosν или

S= C*l*Cos2ν + c*Cosν. (4.37)

Рис.4.26

Для удобства вычислений принимаем второе слагаемое равным с*Cos2ν ; поскольку с величина небольшая (около 30 см), то такая замена не внесет заметной ошибки в вычисления. Tогда

S = (C * l + c) * Cos2ν, или

S = D'* Cos2ν. (4.38)

Oбычно величину (C*l + c) назыывают дальномерным расстоянием. Обозначим разность (D' - S) через ΔD и назовем ее поправкой за приведение к горизонту, тогда

S = D' - ΔD,

где ΔD = D' * Sin2 ν. (4.39)

Угол ν измеряют вертикальным кругом теодолита; причем при 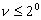поправка ΔD не учитывается. Точность измерения расстояний нитяным дальномером обычно оценивается относительной ошибкой от 1/100 до 1/300.

Кроме обычного нитяного дальномера существуют оптические дальномеры двойного изображения.