Метод узловых потенциалов. В тех случаях, когда в анализируемой схеме число узлов без единицы меньше числа независимых контуров
В тех случаях, когда в анализируемой схеме число узлов без единицы меньше числа независимых контуров, метод узловых потенциалов является более экономичным по сравнению с методом контурных токов.
Суть этого метода состоит в определении напряжений между узлами сложной электрической цепи путём решения системы уравнений, составленных на основе первого закона Кирхгофа. После нахождения неизвестных потенциалов, используя закон Ома, определяют токи во всех ветвях, и выясняют их истинное направление.
Потенциал любой одной точки схемы можно принять равным нулю, так как ток в ветви зависит не от абсолютных значений потенциалов узлов, а от разности потенциалов на концах ветви.
При этом число неизвестных уменьшается с n до n -1.
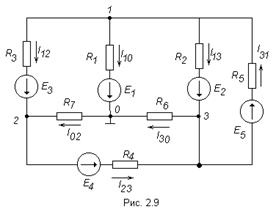Рассмотрим применение данного метода для расчета цепи, приведённой на рис. 2.9, которая имеет большое число ветвей (7) и сравнительно небольшое число узлов (4).
Если узел 0 мысленно заземлить, то есть принять его потенциал равным 0, то неизвестными будут потенциалы только трёх узлов: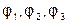 
.
Первоначально в исходной схеме произвольно задаём направления токов, которые обозначаются с двумя индексами: первый индекс определяет номер узла, от которого течет ток, а второй - номер узла, к которому ток подтекает.
Для расчета цепи составляют систему уравнений:
где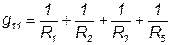 
- сумма проводимостей ветвей, сходящихся в узле 1;
- проводимость ветви, находящейся между узлами
1 и 2, принято всегда брать со знаком «-».
;
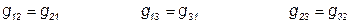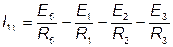- узловой ток первого узла, равный
алгебраической сумме токов, сходящихся в узле.
В образовании узлового тока n-й ветви участвуют лишь те ветви, подходящие к этому узлу, которые содержат источники Э.Д.С. и источники тока.
Если Э.Д.С. и ток источника тока направлены к узлу, то ставится знак «+», в противном случае «-».
После решения системы уравнений определяют токи в ветвях по закону Ома:
; 
; 
;
; 
.
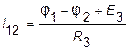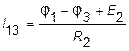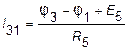В заключении делают проверку на баланс мощностей:
.
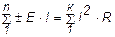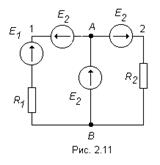
1. Если в ветви находится идеальный источник Э.Д.С. без других сопротивлений, то проводимость такой ветви равна бесконечности (рис. 2.10а). В этом случае применяют следующий приём.
 |
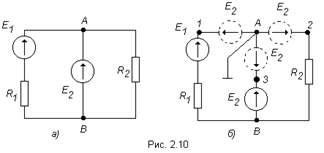В такой ветви встречно данному источнику Э.Д.С. включают такой же источник, Э.Д.С. которого равна первому. Чтобы токи в ветвях не изменялись, в оставшиеся ветви добавляют такие же источники Э.Д.С., направленные от узла а. При этом потенциалы точек 1, 2 и 3 будут равны, то есть могут быть объединены в одну точку А (таким образом, исходная схема в принципе не нарушена). В результате получим схему, изображенную на рис. 2.11.
2.
 |
Если в ветви находится идеальный источник тока, то его проводимость равна нулю
. В этом случае применяют правило переноса источника тока.
В результате такого преобразования в каждом из узлов, значения токов не изменяются. Например, ток в узле b остался неизменным, так как в этот узел добавили и вычли ток J. Из узла а ток J также вытекает, только теперь с другой стороны.
Дата добавления: 2016-02-02; просмотров: 697;