Теорема компенсации
В любой электрической цепи сопротивление можно заменить Э.Д.С., численно равной падению напряжения на этом сопротивлении и направленной встречно току в этом сопротивлении. При такой замене токораспределение в схеме не изменяется.
Для доказательства этой теоремы рассмотрим схему, приведённую на рис. 2.7а, в которой выделим только одну ветвь с сопротивлением R, а всю остальную часть схемы обозначим в виде активного двухполюсника (так как схема, в общем случае, может содержать несколько источников электрической энергии – активных элементов).
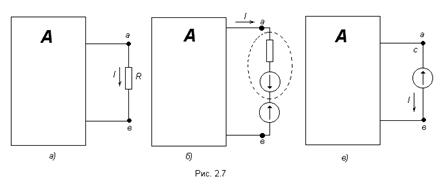 Если теперь в рассматриваемую ветвь включить две одинаковые и противоположно направленные Э.Д.С. Е (рис. 2.7б), численно равные падению напряжения на сопротивлении R
Если теперь в рассматриваемую ветвь включить две одинаковые и противоположно направленные Э.Д.С. Е (рис. 2.7б), численно равные падению напряжения на сопротивлении R 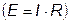 , то ток в цепи не изменится. Это следует из того, что разность потенциалов между точками а и с равна нулю, а значит, напряжение
, то ток в цепи не изменится. Это следует из того, что разность потенциалов между точками а и с равна нулю, а значит, напряжение 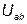 остаётся прежним:
остаётся прежним:
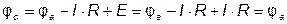 .
.
Так как 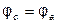






 , то точки а и с можно объединить в одну, то есть закоротить участок ас. При этом получим схему, изображенную на рис. 2.7в.
, то точки а и с можно объединить в одну, то есть закоротить участок ас. При этом получим схему, изображенную на рис. 2.7в.
Таким образом, схемы на рис. 2.7а,в эквивалентны, если 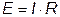 , причем эквивалентная Э.Д.С. Е прямо пропорциональна току I в ветви, то есть зависит от тока.
, причем эквивалентная Э.Д.С. Е прямо пропорциональна току I в ветви, то есть зависит от тока.
ПРИМЕЧАНИЕ:
Любая ветвь с известным током I может быть заменена источником тока 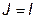 .
.
Дата добавления: 2016-02-02; просмотров: 631;
