Глава III. Основные положения квантовой механики

§ 3.1.Основные сведения из теории операторов.

Из опытов по дифракции и интерференции электронов, а особенно по интерференции одиночных электронов (опыт Юнга), следует, что даже один электрон способен создать интерференционную картину, то есть интерферирует сам с собой. Таким образом, электрон может в одно и то же время находиться в двух различных точках пространства. Очевидно, что понятие траектории для микрочастицы не определено; можно лишь говорить о вероятности нахождения частицы в данный момент времени в данной точке пространства. Одна из основных задач квантовой механики состоит в определении вероятности получения того или иного значения динамических переменных, характеризующих частицу или квантовую систему. Причём в квантовой физике не только координаты и скорости, но и другие физические величины не могут иметь определённые значения. Поэтому говорят лишь о вероятности системы иметь то или иное значение величины её характеризующей: энергии, импульса, координаты и т. д. В связи с эти в квантовой физике физическая величина характеризуется её не численным значением, а оператором, который эта физическая величина представляет.

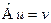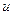Оператором называют правило, по которому любой функции из некоторого пространства сопоставляется другая функция из этого же пространства, то есть . Операторы, используемые в квантовой механике, всегда линейные. Оператор называется линейным, если для произвольных функций и 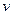, и произвольных постоянных 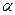и 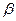выполнено равенство: .

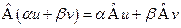Операторы 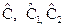называют суммой, разностью и произведением операторов и 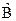соответственно, если справедливы равенства:

,

,

.

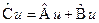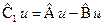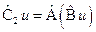При этом произведение операторов в общем случае не коммутативно. Это значит, что 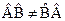. Если же 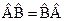, то такие операторы называются коммутирующими. Если 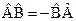, то такие операторы называются антикоммутирующими. Запись 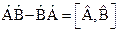называется коммутатором операторов и 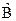. Запись 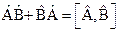называется антикоммутатором операторов и 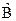. Если результатом действия оператора на функцию 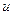является функция 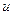, умноженная на некоторое число 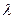, то это число называют собственным значением оператора , а функцию 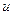– собственной функцией оператора, соответствующей этому собственному значению: 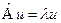. Причём, собственные функции в квантовой механике должны удовлетворять свойствам конечности, непрерывности, однозначности и гладкости. Совокупность собственных значений оператора называется его спектром. Спектр оператора может быть как дискретным, так и непрерывным. Причём, возможны случаи, часть спектра дискретна, а часть непрерывна. Возможны также случаи, когда одному собственному значению соответствует несколько собственных функций. Такое собственное значение называют вырожденным.

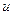Помимо линейности, на квантово-механические операторы накладывается требование самосопряжённости. Оператор называется самосопряжённым или эрмитовым, если для произвольных функций и 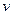справедливо равенство: 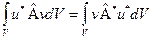1. Это требование обусловлено тем, что собственными значениями самосопряжённых операторов являются действительные числа. Собственные значения, как-либо описывающие физическую величину, измеряются в эксперименте. Вообще говоря, физическую величину можно измерить, если её оператор эрмитовый.

Теорема 1. Собственные функции линейного эрмитового оператора, принадлежащие различным собственным значениям, ортогональны друг другу, то есть 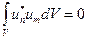, есл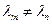и и .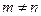

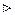Запишем по определению собственного значения: 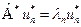и 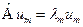(1). Из условия самосопряжённости мы можем записать: 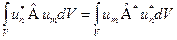. Теперь, подставляя сюда формулы (1), получим: 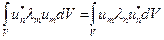. Так как 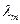и 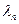– константы, то мы можем вынести их за знак интеграла. Перенося интеграл в левую часть, получим: 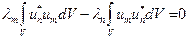, 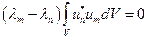. По условию 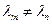, поэтому, 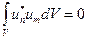. 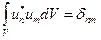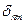Так как собственная функция определяется лишь с точностью до произвольного множителя, то этот множитель можно выбрать так, чтобы функции были ортонормированными: , где – символ Кронекера.

§ 3.2.Постулаты квантовой механики. Представление динамических переменных.

Как и любая область науки, квантовая механика базируется на нескольких основных положениях, принимаемых без доказательства. Эти основные положения сформулированы в виде постулатов.

I постулат. Состояние движения квантового объекта описывается волновой функцией .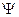

Физический смысл волновой функции в том, что её квадрат есть плотность вероятности обнаружения частицы в данном квантовом состоянии. Плотность вероятности определяется так: 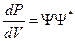, так как функция 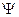комплексна. Тогда вероятность обнаружения частицы в данном квантовом состоянии, описываемом волновой функцией, будет: .

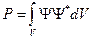II постулат. Волновая функция 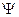подчиняется волновому уравнению: .

Здесь 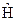– оператор Гамильтона (полной энергии системы), а уравнение, сформулированное во втором постулате, называется уравнением Шредингера.

III постулат. Каждая динамическая переменная представляется определённым линейным эрмитовым оператором.

IV постулат. При изменении некоторой динамической переменной, описываемой оператором , с определённой вероятностью получается одно из собственных значений этого оператора. Вероятность измерения собственного значения 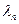равна 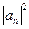, где 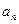есть коэффициент разложения волновой функции 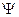по собственным функциям оператора : 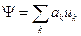. Среднее значение динамической переменной, описываемой оператором в состоянии, описываемом волновой функцией 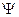, определяется так: .

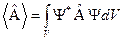Согласно третьему постулату операторы, описывающие динамические переменные, должны быть линейными и эрмитовыми. Однако третий постулат не даёт конкретных значений этих операторов. Вид основных операторов определяется так, чтобы полученные с помощью них значения, совпадали с экспериментальными. Остальные операторы получаются путём формальной замены в функции, описывающей соответствующую величину в классической физике, всех переменных на соответствующие им операторы. Необходимо следить за тем, чтобы полученный оператор оставался линейным и эрмитовым.

1. Оператор координаты есть оператор умножения на эту координату: 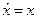, например, .

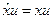2. Оператор проекции импульса на оси декартовой системы координат есть 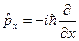, например, 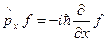. Так как импульс величина векторная, то в векторной форме 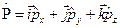. Тогда, после соответствующих преобразований, получим 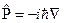. Например, .

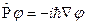3. Оператор полной энергии имеет вид: .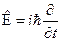

4. Получим теперь уравнение для оператора 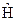. В классической физике функция Гамильтона есть полная энергия системы. Функция Гамильтона выражается через обобщённые координаты так: 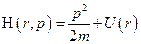– сумма кинетической и потенциальной энергий. Тогда, пользуясь общим правилом, запишем оператор 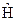: 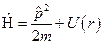, или .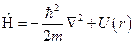

5. Оператор момента импульса. В классической физике 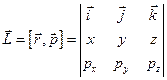. Тогда, расписывая по координатам вектор 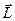, получим: 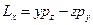; 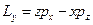и 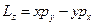. Теперь по общему правилу, производя формальную замену, мы можем записать: 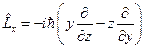, , 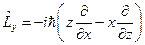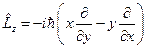. Перейдём теперь к сферической системе координат 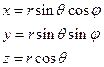(1). Теперь, производя дифференцирование, при переходе к новым переменным, получим: 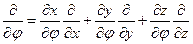. Так как 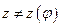, то 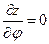. Таким образом, 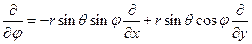. Возвращаясь к формуле (1), мы можем переписать последнее уравнение: 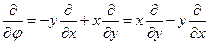. Отсюда для 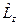имеем уравнение: .

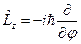§ 3.3. Соотношение неопределённостей Гейзенберга.

Из постулатов квантовой механики следует, что при измерении некоторой физической величины получается определённое значение лишь в том случае, когда волновая функция, описывающая систему, является собственной функцией оператора измеряемой величины. В общем случае различные операторы имеют различные собственные функции, то есть описываемые ими физические величины не могут одновременно иметь точно определённые значения, но в некоторых случаях это возможно. Необходимым и достаточным условием того, чтобы две физические величины имели одновременно определённые значения, является коммутативность операторов, описывающих эти величины. Докажем это утверждение.

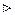Необходимость. Пусть операторы и 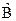имеют общую собственную функцию, а значит описываемые ими физические величины, одновременно имеют определённые значения 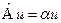, 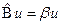. Умножим эти выражения на 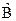и соответственно: 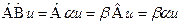, 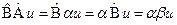. Отнимем из первого второе выражение: 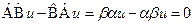. Так как по условию функция 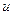не нулевая, то 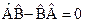, то есть операторы и 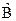коммутирующие.

Достаточность. Пусть 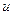– собственная функция оператора 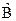: 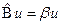. Если операторы и 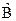коммутирующие, то 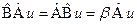, то есть функция 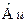является собственной функцией оператора 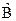, отвечающая собственному значению 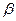. Но такой функцией является функция 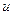. Следовательно, функция 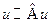совпадает с точностью до произвольного постоянного множителя с функцией 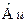. Этим множителем может быть 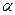: 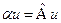. Отсюда функция 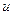является собственной функцией оператора , соответствующая собственному значению 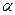, а значит, операторы и 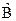имеют общую собственную функцию 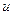, и поэтому соответствующие им динамические переменные являются одновременно измеримыми с какой угодно степенью точности.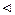

Проверим, являются ли одновременно измеримыми проекция импульса на координату и сама эта координата: 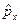и 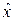. Найдём их коммутатор: 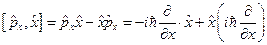. Подействуем этим оператором на функцию 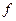: 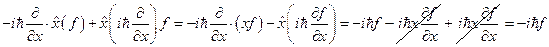. То есть оператор коммутатора не равен нулю. Значит операторы 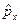и 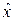не коммутирующие. Значит, координата и проекция импульса не могут одновременно иметь определённые значения.

Соотношение между дисперсией координаты и импульсом частицы было установлено Гейзенбергом (1927 г.) и получило в последствии название соотношения неопределённостей Гейзенберга. Найдём его. По определению дисперсии мы можем записать1 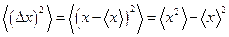. Аналогично для импульса: 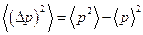. Выберем такую систему координат, в которо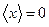й и 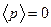. В этой системе координат дисперсия координаты и импульса будет выглядеть так: 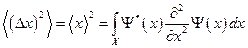и 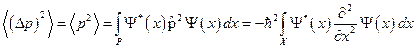. Для нахождения связи между неопределённостью координаты и неопределённостью импульса, Гейзенберг предложил рассмотреть интеграл вида: 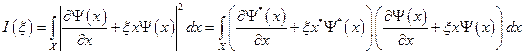. Раскроем теперь скобки и приведём подобные члены. Причём, запишем полученное выражение как многочлен относительно степеней 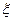: 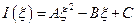. Так как подынтегральное выражение являлось квадратом модуля, то интегральная функция 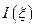будет положительно определена: 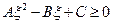(1). Запишем теперь выражения для коэффициентов многочлена (1): 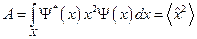(см. определение дисперсии); 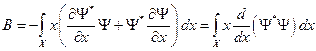. Беря полученный интеграл по частям, запишем: 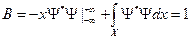. Первое слагаемое здесь равно нулю2, а второе 1 в силу условия нормировки. 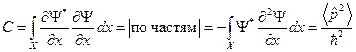. Запишем теперь условие положительной определённости (1): дискриминант (1) должен быть меньше либо равен нулю: 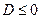, , 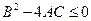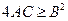. Подставляя в последнее выражение значения 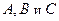, получим: 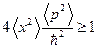; 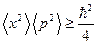. Возвращаясь к определению дисперсии в выбранной нами системе координат, мы можем записать: 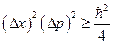. Или, извлекая корень, 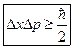. Данное соотношение носит название соотношения неопределённостей Гейзенберга. Оно показывает, что импульс и координаты частицы не могут быть одновременно определены (измерены) со сколь угодно большой точностью, хотя любая из этих величин по отдельности измерима с любой точностью. До измерения частица не имела определённых значений динамических переменных. Определённые значения динамические переменные квантовой системы принимают только в процессе измерения. Под процессом измерения в квантовой физике понимается процесс взаимодействия с любым классическим объектом (прибором). Наличие же наблюдателя вовсе не обязательно. Таким образом, измерения объективны.

§ 3.4. Соотношение неопределённостей произвольных физических величин. Принцип дополнительности.

Соотношение неопределённостей аналогичное соотношению неопределённостей Гейзенберга можно получить для произвольной физической величины. Рассмотрим две произвольные физические величины, описываемые операторам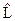и и 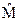, коммутатор которых равен: 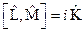. Введём величину 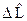, которая есть отклонение оператора 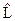от его среднего значения: 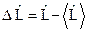и, соответственно, 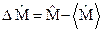. Аналогично Гейзенбергу рассмотрим интеграл вида: 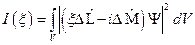. Так как под интегралом стоит квадрат модуля, то он должен быть положительно определённым оператором функции 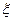. Если операторы описывают физическую величину, то они должны быть линейными и эрмитовыми. Используя условие самосопряжённости операторов 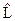и 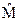, и определение среднего, мы получим: 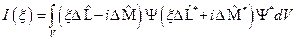. Вспоминая условие эрмитовости, мы можем записать: 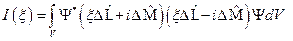; 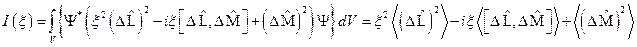. Полученное соотношение, после выполнения условия положительной определённости интеграла даст нам соотношение неопределённостей для произвольных физических величин, описываемых операторам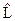и и .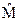

Для описания квантовой системы невозможно пользоваться всеми теми величинами. Которые используются в классической физике, то есть часть из этих величин всегда не будет определена достаточно точно. Это утверждение носит название принципа дополнительности.

§ 3.5. Понятие представления в квантовой механике.

Как уже было ранее сказано, мы можем разложить любую функцию по полному ортогональному набору других функций (например, в ряд Фурье), то есть: 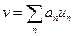, причём набор коэффициентов разложения 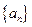полностью определяет функцию 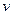. Мы доказали, что собственные функции линейного эрмитового оператора образуют полный ортонормированный базис, то есть любую функцию можно разложить по собственным функциям этого оператора. Разложение функции по полной системе собственных функций оператора является переводом её функционального представления в так называемое – представление. В квантовой механике говорят: «Переведём функцию в – представление». Не только функции, но и операторы могут быть записаны в различных представлениях.

Пусть функция 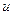есть результат действия оператора 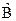на функцию 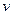: 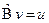(1). Запишем разложение функци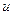й и 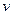по собственным функциям оператора , то есть переведём их в – представление: .

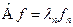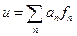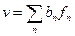; , где 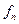– собственные функции оператора . Подставляя два последних равенства в (1), получим: 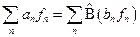. Умножим на 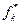последнее выражение: 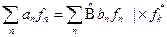, 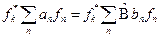; 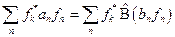. Так как 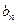численный множитель, то мы можем поменять его местами с функцией 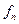: 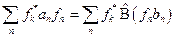. Проинтегрируем теперь обе части по всей области изменения 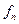, то есть по объёму: 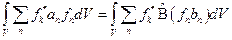. Так как операции интегрирования и суммирования коммутативны, то мы можем изменить порядок действий в последней формуле: 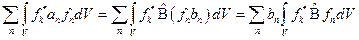(2). Введём некоторые обозначения: 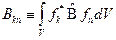. Величину 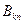называют матричным элементом оператора 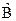. 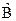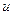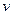Матричный элемент оператора связывает функции и в – представлении. 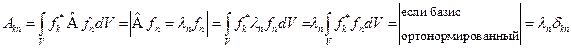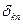Найдём матричные элементы оператора в его собственном представлении, , где – символ Кронекера. Таким образом, матричные элементы оператора в его собственном представлении образуют диагональную матрицу. Вернёмся к равенству (2). После суммирования по 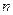получим слева некоторую функцию 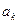, которая не зависит от 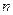. Тогда мы можем записать: 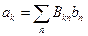. 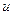Полученное соотношение отражает связь между коэффициентами – представления функций и .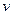

В квантовой механике используются различные виды представлений. Чаще всего используется координатное или 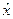– представление. В нём все функции раскладываются по собственным функциям оператора координат – оператора 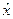. Реже используется 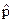– представление, где функции раскладываются по собственным функциям оператора импульса. Существует также 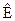– представление. В этом случае все функции раскладываются по собственным функциям оператора Гамильтона.