Оценка параметров уравнения регрессии при ПЛР
Истинное уравнение ПЛР 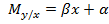 , отображаемое в общем виде, в частности, таблицей 2, неизвестно (всю генеральную совокупность наблюдать невозможно). Можно только по имеющейся выборке экспериментальных данных оценить генеральные параметры α и β.
, отображаемое в общем виде, в частности, таблицей 2, неизвестно (всю генеральную совокупность наблюдать невозможно). Можно только по имеющейся выборке экспериментальных данных оценить генеральные параметры α и β.
Итак, имеется экспериментально определенная выборка объема n, представляющая собой пары (xi;yi) - наблюдений зависимой величины Y, соответствующей значениям независимой переменной x.
Оценки генеральных параметров α и β обозначаются соответственно a и b:
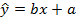 , ,
| (7) |
соответственно, 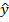 - это оценка.
- это оценка.
Для их определения чаще всего используется метод наименьших квадратов (МНК).
Отметим, что, как показано на рис.9, прямую через экспериментальные данные можно провести по разному.
| x |
| y |
| Рис.9 |
Суть МНК заключается в следующем: искомая функция (7) должна быть построена так, чтобы сумма квадратов отклонений (рис.10) у- координат всех экспериментальных точек от у- координат графика функции была бы минимальной, то есть рассматривается для каждой точки разность отмеченных у- координат:
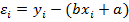 . .
| (8) |
Тогда минимизируемая сумма запишется в виде функции:
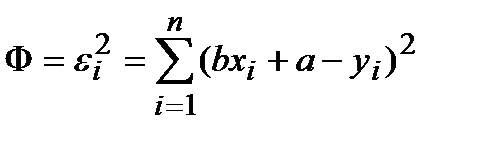 . .
| (9) |
| εi |
| y |
| x |
| Рис.10 |
| yi |
| xi |
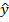 =bxi+a =bxi+a
|
Почему сводятся к минимуму квадраты ошибок, а не сами ошибки? Дело в том, что в большинстве случаев ошибки бывают в обе стороны: оценка может быть больше измерения или меньше его. Если складывать ошибки с разными знаками, то они будут взаимно компенсироваться, и в итоге сумма даст нам неверное представление о качестве оценки. Часто для того, чтобы итоговая оценка имела ту же размерность, что и измеряемые величины, из суммы квадратов ошибок извлекают квадратный корень.
Далее находится минимум выражения (9). Для этого приравнивают к нулю частные производные 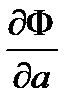 и
и 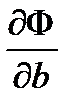 , и получают формулы для нахождения неизвестных коэффициентов:
, и получают формулы для нахождения неизвестных коэффициентов:
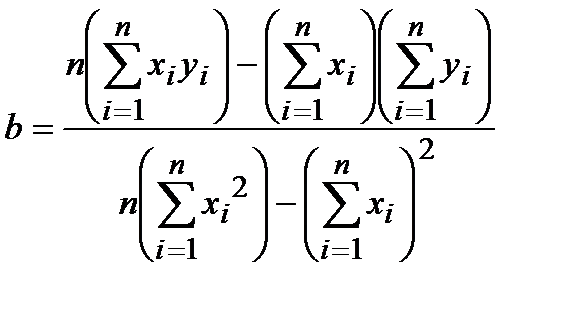
| (10) |
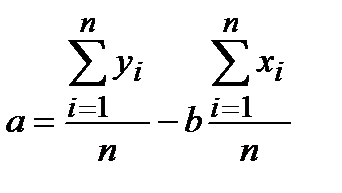
| (11) |
Если уравнение прямой ищется в виде y = bx, то верна следующая формула:
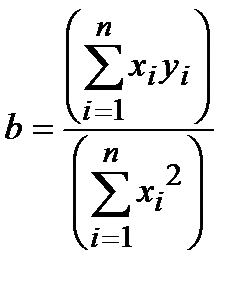
| (12) |
Пример
Данные экспериментальных исследований:
| x | 1,5 | 1,9 | 2,3 | 2,5 | 2,8 | ||
| y | 4,4 | 2,7 | 2,3 | 0,3 | -0,5 | -0,9 |

Таким образом, искомая прямая имеет вид : 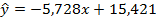 ,
,
Дата добавления: 2016-01-30; просмотров: 717;
