Классификация погрешностей по закономерности их изменения и по способам регулировки
Погрешности постоянные (аддетивные)
ΔS
Sa So Sb S
Так выглядит погрешность начального положения в рычажных механизмах, которая приводит к несимметричности градуировочной характеристики. Погрешность может быть скомпенсирована, для этого вводится постоянный компенсатор. Система регулировки заключается в следующем: с помощью измерительного устройства измеряем любое значение So в пределе от Sa до Sb. Это значение точно соответствует тому, которое необходимо знать в соответствии с градуировочной характеристикой.
Прогрессивные (мультипликативные).
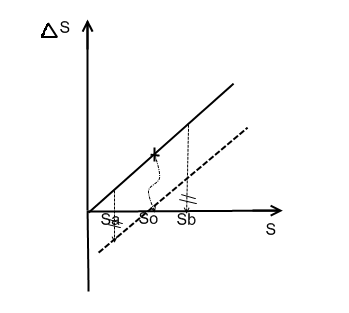
К таким погрешностям относятся все погрешности масштабов, погрешности, вызванные отклонением длин рычагов, отклонения значений электрических сопротивлений. Частичная компенсация погрешности производится введением постоянного компенсатора. Опустив прямую, необходимо сделать ее симметричной относительно оси абсцисс, чем мы максимально уменьшаем значение погрешности по модулю. Для полной компенсации вводится масштабный компенсатор, который в состоянии уменьшить передаточное отношение. Например: изменение длины рычага в аналитических весах. Такой компенсатор позволяет регулировать длины плеч весов. Регулировка осуществляется в двух точках (можно брать 2 любые точки).
Нелинейные
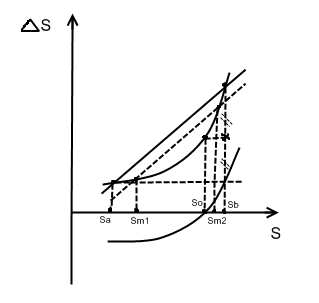
Под нелинейной погрешностью понимается погрешность монотонно убывающая или возрастающая, но изменяющаяся нелинейно. Она частично может быть скомпенсирована введением постоянного компенсатора. Отыскиваем So, для чего делим максимальную ординату пополам, поэтому метод называется половинения погрешности. На практике вводят компенсатор и определяют погрешности по краям шкалы. Когда они становятся равными по краям шкалы и противоположными по знаку, регулировку прекращают.
Sm1, Sm2- определяют апроксимирующую прямую
Sa =Sm1, Sb =Sm2, т.е. вводят масштабный компенсатор так, чтобы по краям шкалы погрешности были нулевые. Для полной компенсации должен вводиться и третий компенсатор, но на практике обычно обходятся двумя, т.е. компенсация частичная.
Дата добавления: 2016-01-29; просмотров: 762;
