Диполь в однородном и неоднородном электрических полях

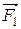Если диполь поместить в однородное электрическое поле, образующие диполь заряды +q и –q окажутся под действием равных по величине, но противоположных по направлению сил и .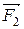

Рис. 14.2.

Эти силы образуют пару, плечо которой равно l·sina, т.е. зависит от ориентации диполя относительно поля. Модуль каждой из сил равен q×E. Умножив его на плечо, получим величину момента пары сил, действующей на диполь:

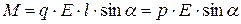, (14.1)

где р – электрический момент диполя.

Формулу (14.1) можно записать в векторном виде:

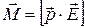. (14.2)

Вращающий момент 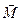стремится повернуть диполь так, чтобы его дипольный момент 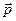установился по направлению поля.

Чтобы увеличить угол между векторам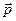и и 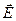на 2a, нужно совершить против работу сил, действующих на диполь в электрическом поле:

.

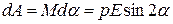Эта работа идет на увеличение потенциальной энергии W, которой обладает диполь в электрическом поле:

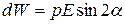. (14.3)

Интегрируя (14.3) получим выражение для энергии диполя в электрическом поле:

.

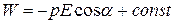Наконец, полагая const равной нулю, получаем

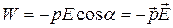. (14.4)

Выбор Сonst=0соответствует положению диполя перпендикулярно полю. Наименьшее значение энергии, равное –рЕ, получается при ориентации диполя по направлению поля, наибольшее, равное рЕ, - при ориентации против поля.

В неоднородном поле силы, действующие на заряды диполя, не одинаковые по величине. При малых размерах диполя силы 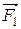и 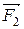можно считать коллинеарными. Предположим, что поле быстрее всего изменяется в направлении х, совпадающем с направлением 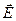в том месте, где расположен диполь. Положительный заряд диполя смещен относительно отрицательного в направлении х на величину .

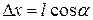Рис. 14.3.

Поэтому напряженность поля в точках, где помещаются заряды, отличается на .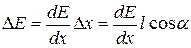

Следовательно, результирующая 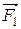+ 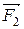сил, действующих на диполь, будет отлична от нуля. Проекция этой результирующей на ось х, очевидно равна:

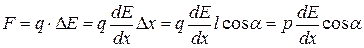. (14.5)

Таким образом, в неоднородном поле на диполь кроме вращательного момента (14.2) действует сила (14.5), под действием которой диполь либо втягивается в область более сильного поля (угол a острый), либо выталкивается из нее (угол a тупой).