Кинетическая энергия вращения

Рассмотрим абсолютно твердое тело, вращающееся около неподвиж­ной оси z, проходящей через него (рис.4.8). Мысленно разобьем это тело на маленькие объемы с элементарными мас­сами m₁, m₂, ..., т_n, находящиеся на рас­стоянии r₁, r₂ , ..., r_n от оси вращения. При вращении твердого тела относительно не­подвижной оси отдельные его элементар­ные объемы массами m_i опишут окружно­сти различных радиусов r_i, и имеют раз­личные линейные скорости u_i. Но так как мы рассматриваем абсолютно твердое те­ло, то угловая скорость вращения этих объемов одинакова:

ω = υ₁/ r₁ = υ₂/ r₂ = … = υ_n/ r_n . (4.8)

Кинетическую энергию W_вр вращающегося тела найдем как сумму кинетических энер­гий его элементарных объемов:

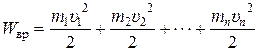
или

.

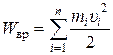Используя выражение (4.5), получим

,

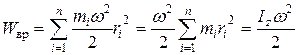где I_z - момент инерции тела относитель­но оси z. Таким образом, кинетическая энергия вращающегося тела

W_вр= I_zω²/2. (4.9)

Из сравнения формулы (4.6) с вы­ражением для кинетической энер­гии тела, движущегося поступательно (W_к = mυ²/2), следует, что момент инерции вращательного движения - мера инер­тности тела. Формула (4.9) справедлива для тела, вращающегося вокруг непод­вижной оси.

В случае плоского движения тела, на­пример цилиндра, скатывающегося с на­клонной плоскости без скольжения, энер­гия движения складывается из энергии поступательного движения и энергии вра­щения:

W = mυ_c²/2 + I_cω²/2, (4.10)

где m - масса катящегося тела; υ_c - ско­рость центра масс тела; I_c - момент инерции тела относительно оси, проходя­щей через его центр масс; ω - угловая скорость тела.