Уравнение динамики вращательного движения твердого тела

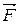Найдем выражение для работы при вращении тела (рис.4.9). Пусть сила приложена в точке В, находящейся от оси вращения на расстоянии ά - угол между направлением силы и радиусом-вектором . Так как тело абсолютно твер­дое, то работа этой силы равна работе, затраченной на поворот всего тела. При повороте тела на бесконечно малый угол dφ точка приложения В проходит путь ds = rdφ, и работа равна произведению проекции силы на направление смещения на величину смещения:

δA = F sinά rdφ .

Учитывая (4.1), можем записать δA = M_z dφ,

где Fr sinά = Fl = M_z - момент силы от­носительно оси z. Таким образом, работа при вращении тела равна произведению момента действующей силы на угол пово­рота.

Работа при вращении тела идет на увеличение его кинетической энергии:

δA = dW_к,

но

dW_к = d(I_z ω²/2) = I_z ω dω

поэтому

M_z dφ = I_z ω dω

или

.

Учитывая, что 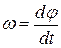, получим

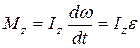. (4.11)

Уравнение (4.11) представляет собой уравнение динамики вращательного дви­жения твердого телаотносительно непод­вижной оси.

Можно показать, что если ось враще­ния совпадает с главной осью инерции, проходящей через центр масс, то имеет место векторное равенство

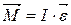,(4.12)

где I - главный момент инерции тела (момент инерции относительно главной оси).