Граничные условия при наличии заряженных поверхностей.
Предположим, что заряд расположен на некоторой поверхности и удерживается на ней некоторыми силами. Пусть  - плотность
- плотность
поверхностного заряда. Тогда  - заряд на элементе
- заряд на элементе 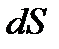 .
.
Можно заметить, что напряжённость поля
| σ |
в противоположные стороны. Напряженность поля
испытывает скачок, то есть не непрерывна.
Уравнения, связывающие напряженности полей
по разные стороны поверхности называются
граничными условиями.
Граничные условия для нормальной компоненты Е
Найдем их с помощью уравнения: Гаусса:
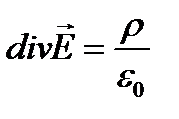 или
или
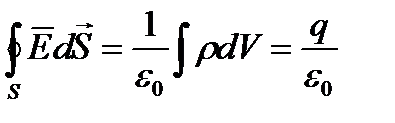
В качестве замкнутой поверхности S возьмём цилиндр, пересеченный поверхностью, высотой h и основаниями S1 и S2.. Выберем нормаль 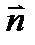 из 1 в 2 .
из 1 в 2 .
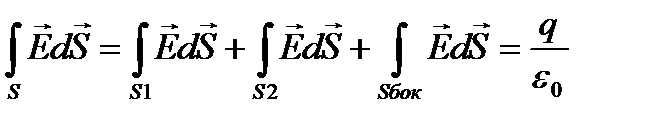
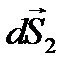
| S0 |
Так как 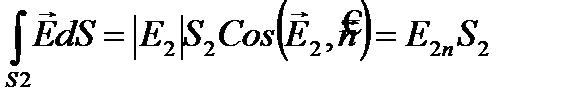
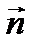
т. к. мы считаем, что 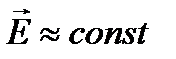 , т. е. цилиндр мал.
, т. е. цилиндр мал.
h
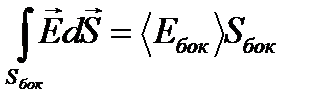 «теорема о среднем».
«теорема о среднем».
Таким образом, 

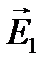
Очевидно, что при 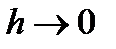
 т. е.
т. е. 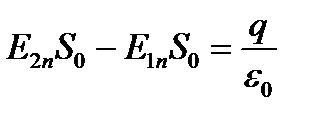 ,но
,но 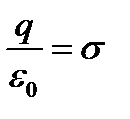

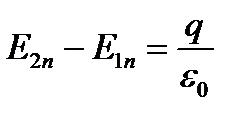 (2.1)
(2.1)
Таким образом, скачок нормальной составляющей полностью
определяется поверхностной плотностью заряда σ.
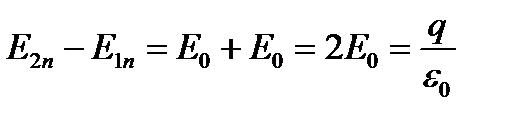 σ
σ 
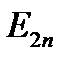
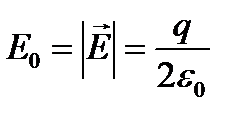 - поле бесконечной плоскости. (2.2)
- поле бесконечной плоскости. (2.2) 
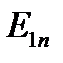
Дата добавления: 2016-01-29; просмотров: 1143;
