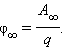Потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.

Потенциал φ_∞ поля точечного заряда Q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом:

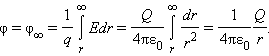
Как следует из теоремы Гаусса, эта же формула выражает потенциал поля однородно заряженного шара (или сферы) при r ≥ R, где R – радиус шара.

Для наглядного представления электростатическое поля наряду с силовыми линиями используют эквипотенциальные поверхности.

Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала.

Силовые линии электростатическое поля всегда перпендикулярны эквипотенциальным поверхностям.

Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы. На рис. 1.4.3 представлены картины силовых линий и эквипотенциальных поверхностей некоторых простых электростатических полей.

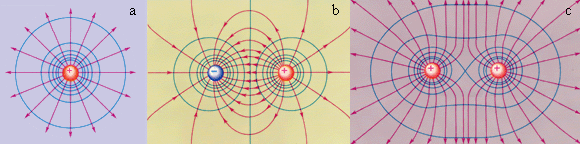
Рисунок 1.4.3. Эквипотенциальные поверхности (синие линии) и силовые линии (красные линии) простых электрических полей: a – точечный заряд; b – электрический диполь; c – два равных положительных заряда

В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей.

Если пробный заряд q совершил малое перемещение 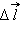вдоль силовой линии из точки (1) в точку (2), то можно записать:

где Δφ = φ₁ – φ₂ – изменение потенциала. Отсюда следует

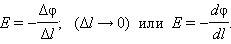
Это соотношение в скалярной форме выражает связь между напряженностью поля и потенциалом. Здесь l – координата, отсчитываемая вдоль силовой линии.

Из принципа суперпозиции напряженностей полей, создаваемых электрическими зарядами, следует принцип суперпозиции для потенциалов: