Момент импулься и закон сохранения момента импульса

Закон сохранения момента импульса.

Зако́н сохране́ния моме́нта и́мпульса (закон сохранения углового момента) — один из фундаментальных законов сохранения. Математически выражается через векторную сумму всех моментов импульса относительно выбранной оси для замкнутой системы тел, которая остается постоянной, пока на систему не воздействуют внешние силы. В соответствии с этим момент импульса замкнутой системы в любой системе координат не изменяется со временем.

Закон сохранения момента импульса есть проявление изотропности пространства относительно поворота.

В упрощённом виде: 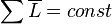, если система находится в равновесии.

Момент импулься и закон сохранения момента импульса

акон сохранения момента импульса является следствием закона сохранения углового момента, который, в свою очередь, является следствием закона сохранения энергии системы. Поэтому неверно, когда закон сохранения момента импульса считают основным законом сохранения наравне с законом сохранения энергии. Следствие не может быть поставлено наравне с причиной, его вызывающей.

1. Вывод закона сохранения углового момента составной системы
с применением теоремы Штайнера.

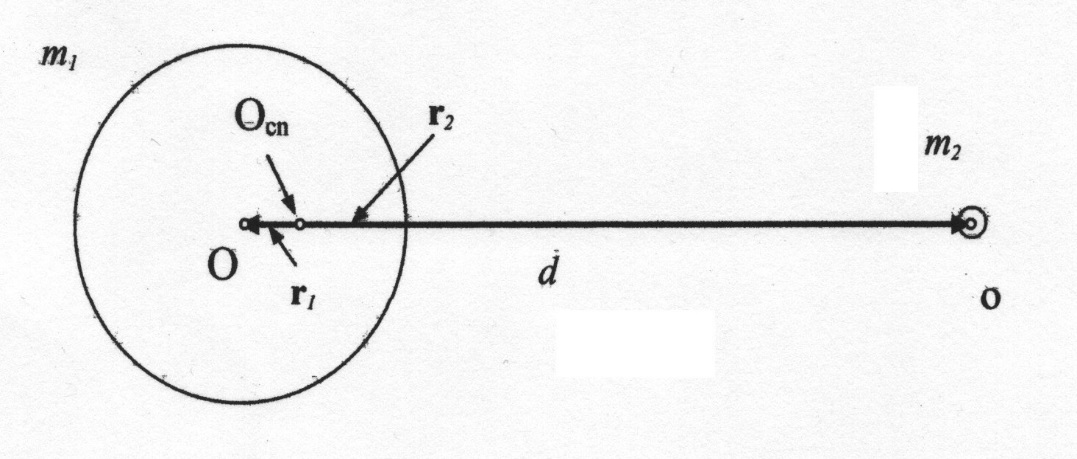Рассмотрим простейший вариант, показанный на рисунке, когда система состоит из двух тел с массами m₁ и m₂ , причем m₂ < m₁ . Расстояние между центрами масс двух тел равно d. Центр вращения системы из двух тел О_cn лежит на прямой, соединяющей центры масс Ои о.

Пусть оба тела вращаются вокруг собственных центров с угловыми скоростями ω₁ и ω₂ . Одновременно с этим пусть система из двух тел вращается с угловой скоростью ω вокруг общего центра системы О_cn , который находится на оси Оz, перпендикулярной плоскости рисунка. Соответственно, и псевдовекторы ω, ω₁ и ω₂ также перпендикулярны плоскости рисунка.

Момент инерции J_zi (вращательную инертность) i-го тела при вращении вокруг оси Оz при этих условиях можно определить по теореме Штайнера

J_zi = J_zsi + m_i r_i² , ( 1 )

где J_zsi – собственный момент инерции i–го тела относительно своей оси вращения, параллельной оси Оz; m_i– масса i–го тела; r_i – расстояние от общей оси вращения до собственной оси вращения i–го тела.

Если векторы угловых скоростей ω₁ и ω₂ не параллельны друг другу и вектору угловой скорости всей системы ω, то каждый из векторов ω₁ и ω₂ следует разложить на два вектора: параллельный и перпендикулярный вектору ω. Теорема Штайнера учитывает только компоненты векторов ω₁ и ω₂ , параллельные вектору ω.

В статье, посвященной угловому моменту вращающейся системы, приведено определяющее уравнение для закона сохранения углового момента твердого тела в виде L_z = J_zω = const. Подставив сюда выражение для момента инерции i–го тела J_zi из уравнения (1), мы приходим к закону сохранения углового момента системы из двух тел, изображенной на рисунке:

L_z = [(J_zs)₁ + m₁ r₁²] ω + [(J_zs)₂ + m₂ r₂²] ω = const . ( 2 )

Естественно, что аналогичное уравнение может быть получено для системы, состоящей из скольких угодно составных частей.

2. Как мы приходим к понятию "момент импульса" системы.

Предположим, что собственные моменты инерции тел (J_zs)_i пренебрежимо малы по сравнению со вторыми слагаемыми в теореме Штайнера, то есть предположим, что собственными угловыми моментами тел, составляющих систему, можно пренебречь. Тогда закон сохранения углового момента системы (2) можно будет переписать в виде

L_z = m₁ r₁²ω + m₂ r₂²ω = const . ( 3 )

Угловая скорость системы из нескольких тел может быть определена по любой из составных частей системы по уравнению

ω = [e_ri (v_τi /r )] , ( 4 )

где v_τi − касательная скорость центра вращения i-го тела относительно общего центра вращения О_cn; e_ri − орт i-го радиуса, проведенный из точки О_cn . Закон сохранения углового момента системы в виде (3) после введения в него угловой скорости по уравнению (4) запишется в виде:

L_z = m₁ r₁ [e_r v_τ1 ] + m₂ r₂ [e_r v_τ2 ] = const . ( 5 )

Введем скалярные величины m и r в квадратные скобки. Учитывая, что re_r = r, и умножив скаляр m на вектор v, мы приходим к уравнению

L_z = [r₁ (m₁ v_τ1 )] + [r₂ (m₂ v_τ2 )] = const . ( 6 )

Векторную величину (mv), присутствующую в уравнении (6), называют в физике импульсом и обозначают символом p. А величину [r p] = [r (mv)] называют в физике моментом импульса. Ее тоже обозначают символом L_z , то есть тем же символом, который применяют для обозначения углового момента. Но при этом не учитывают, что к уравнению (6) мы пришли при пренебрежении собственными моментами инерции тел. Подобное умолчание и является причиной того, что между угловым моментом и моментом импульса часто, но не обосновано, ставят знак равенства.

Размерность момента импульса совпадает с размерностью углового момента, так как закон сохранения момента импульса (6) вытекает из закона сохранения углового момента (2). В СИ размерность момента импульса равна L²МT⁻¹, а единица равна кг м² с^-1. Та же размерность в системе величин ЭСВП выглядит как EА⁻¹T, а единица равна Дж об^-1 с. Подробнее об этих размерностях и единицах рассказано в статье, посвященной угловому моменту.