Поступательное движение. Рассмотрим движение материальной точки вдоль произвольной кривой (рисунок 2).

Рассмотрим движение материальной точки вдоль произвольной кривой (рисунок 2).

Траектория – линия, описываемая материальной точкой при движении в пространстве от точки (1) до точки (2). В зависимости от формы траектории движение бывает прямолинейным или криволинейным.

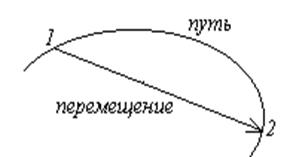
Рисунок 2 – Определение пути и перемещения

Перемещение 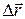– вектор, соединяющий начальную (1) и конечную (2) точки траектории, по которой двигалась материальная точка некоторый промежуток времени.

Путь – сумма длин отрезков траектории от точки (1) до точки (2).

При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и модуль перемещения равен пройденному пути Δs.

Для характеристики движения материальной точки вводится векторная величина – скорость, которая определяет быстроту и направление движения. Модуль скорости равен производной пути по времени:

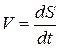. (2.1.1)

Мгновенная скорость направлена по касательной к траектории. В системе СИ скорость измеряется в м/с.

Физической величиной, характеризующей быстроту изменения скорости по модулю и направлению, является ускорение:

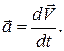(2.1.2)

В системе СИ ускорение измеряется в м/с².

Скорость тела может изменяться как по величине (модулю), так и по направлению. Вектор ускорения принято представлять в виде двух составляющих: тангенциальной и нормальной (рисунок 3).

Тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю:

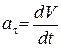. (2.1.3)

Тангенциальное ускорение направлено по касательной к траектории параллельно вектору скорости в случае ускоренного движения и в противоположную сторону в случае замедленного.

Нормальная составляющая ускорения характеризует быстроту изменения скорости по направлению. Нормальное ускорение направлено к центру кривизны траектории и численно равно

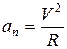, (2.1.4)

где R - радиус кривизны траектории в данной точке.

Рисунок 3 – Определение составляющих ускорения

(ускоренное движение)

Вектор нормального ускорения и вектор тангенциального ускорения направлены перпендикулярно друг другу. Вектор полного ускорения

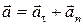, , (2.1.5)