Динамика вращательного движения

Опыт показывает, что при вращательном движении важно не только значение массы тела, но и ее распределение относительно оси вращения. Мерой инертности тела при вращательном движении является момент инерции. Моментом инерции материальной точки массой m называется физическая величина, равная

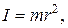(2.1.13)

где r - расстояние от материальной точки до оси вращения.

Момент инерции твердого тела равен сумме моментов инерции составляющих тело материальных точек:

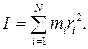(2.1.14)

Здесь r_i - расстояние материальной точки массой m_i до оси вращения.

Моменты инерции некоторых тел правильной геометрической формы относительно оси, проходящей через центр масс тела, можно найти в справочнике. Момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера: момент инерции тела I относительно произвольной оси

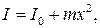(2.1.15)

где I₀ - момент инерции тела относительно оси, проходящей через центр масс параллельно заданной оси, x - расстояние между осями.

Моментом силы относительно некоторой точки О называется векторная величина, равная векторному произведению радиус-вектора точки приложения силы на силу

, (2.1.16)

где 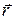- радиус-вектор точки приложения силы, проведенный из точки О. Численное значение момента силы

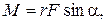(2.1.17)

где α – наименьший угол между направлениям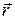и и 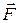. Вектор момента силы перпендикулярен плоскости, в которой лежат радиус-вектор и вектор силы, направление момента силы находится по правилу правого винта.

Кратчайшее расстояние от оси вращения до линии действия силы называется плечом силы. Величину момента силы можно определить как произведение силы F на ее плечо l

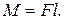(2.1.18)

Единица измерения момента силы Н×м.

Для равновесия тела, имеющего неподвижную ось вращения, необходимо, чтобы алгебраическая сумма моментов всех сил, действующих на тело, относительно этой оси была равна нулю:

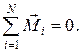(2.1.19)