Резервуары с постоянной толщиной стенки

Толщина боковых стенок резервуаров ограничивается ми­нимальным значением δ₀ из условия устойчивости, т.е. недопу­щения самопроизвольного смятия стенок пустого резервуара. Эта минимальная толщина равна 4 мм. Если размеры резервуара та­ковы, что в заполненном состоянии напряжения у нижней кромки резервуара не превышают допустимых для листов металла с ми­нимальной толщиной δ₀, то такие резервуары сооружают с по­стоянной толщиной стенки.

В объем металла V_M, необходимого для строительства ре­зервуара, входят:

— объем металла днища и кровли

V_d,_K,=π · R² · (δ_d+δ_K)= π ·R² · λ,

где λ = δ_д + δ_К; δ_д и δ_К - толщины листов днища и кровли;

— объем металла боковых стенок резервуара

V_б=2 · π · R ·H · δ₀.

Тогда V_M= π · R² · λ + 2 · π · R · H · δ₀ /

Так как

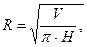(9.1)

где V = π · R² · H, то

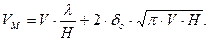
Минимальный объем металла, затрачиваемого на резерву, ар, найдем из условия dV_M /dH = 0

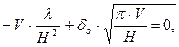
после преобразований получаем

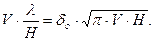(9.3)

Сопоставляя (9.3) и (9.2), видим, что левая часть уравнения — это объем металла днища и кровли, а правая — половина объ­ема металла боковых стенок резервуара. Следовательно, резер­вуар с постоянной толщиной стенки имеет наименьший объ­ем металла, когда объем металла днища и кровли в два раза меньше объема металла стенок.

Из уравнения (9.3) находим оптимальную по затрате метал­ла высоту резервуара

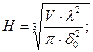(9.5)

Подставим в (9.1) значения Н и R из (9.4) и (9.5), получим объем металла в резервуаре с оптимальными параметрами

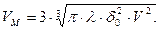
Условие прочности для вертикальных тонкостенных ци­линдрических сосудов на основании уравнения Лапласа

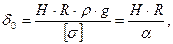
где а = [σ]/(р · g); р — плотность продукта; g - ускорение свободного падения; [σ] - допускаемое напряжение материала стенок.

Подставив в (9.6) значения Н и R из (9.4) и (9.5), получим

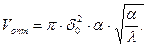(9.7)